当m= 时,抛物线y=mx2+2(m+2)x+m+3的对称轴是y轴;当m= 时,图象与y轴交点的纵坐标是1;当m= 时,函数的最小值是-2.
【答案】
分析:①由于对称轴是y轴即对称轴是x=0,把系数代入公式x=
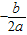
得即可求出m;
②求函数与y轴的交点时,令x=0,得到y=m+3=1,由此可以求出m;
③当m>0时函数有最小值,且最小值是:

=-2由此可以求出m.
解答:解:①∵抛物线y=mx
2+2(m+2)x+m+3的对称轴是y轴
∴x=-
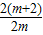
=0
解得:m=-2
当m=-2时,抛物线y=mx
2+2(m+2)x+m+3的对称轴是y轴
②令x=0,得到y=m+3=1
∴m=-2
∴当m=-2时,图象与y轴交点的纵坐标是1
③∵函数的最小值
而最小值是:

=-2
解得m=4
当m=4时,函数的最小值是-2.
点评:本题考查的是二次函数的增减性及顶点坐标、对称轴的解答方法.

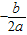 得即可求出m;
得即可求出m; =-2由此可以求出m.
=-2由此可以求出m.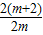 =0
=0 =-2
=-2
