
【题目】如图,在菱形![]() 中,
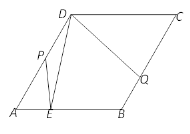
中,![]() =60°, AB=2,点E是AB上的动点,作∠EDQ=60°交BC于点Q,点P在AD上,PD=PE.
=60°, AB=2,点E是AB上的动点,作∠EDQ=60°交BC于点Q,点P在AD上,PD=PE.
(1)求证:AE=BQ;
(2)连接PQ, EQ,当∠PEQ=90°时,求![]() 的值;
的值;
(3)当AE为何值时,△PEQ是等腰三角形.
【答案】(1)见解析;(2)![]() =
=![]() ;(3)AE为
;(3)AE为![]() 或2
或2
【解析】
(1)连结DB,根据“ASA”证明△ADE≌△BDQ即可;
(2)先证明△DEQ是等边三角形,可得∠DEQ=60°,进而可证明∠AED=90°,根据勾股定理求出DE的长,根据两平行线间的距离相等求出PQ的长,即可求出![]() 的值;
的值;
(3)分三种情况讨论求解:①当QP=QE时,②当PE=QE时,③当PE=PQ时.
解:(1)连结DB,
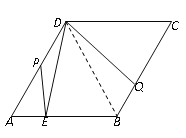
∵四边形ABCD为菱形,∠A=60°,
∴AD=AB=DB,∠DBQ=∠A=60°.
∴∠ADB=60°.
∵∠EDQ=60°,
∴∠ADE=∠BDQ.
∴△ADE≌△BDQ.
∴AE=BQ.
(2)如图,

∵△ADE≌△BDQ,
∴DE=DQ.
∵∠EDQ=60°,
∴△DEQ是等边三角形,
∴∠DEQ=60°,DE=EQ=DQ.
∵∠PEQ=90°,
∴∠PED=30°.
∵PD=PE,
∴∠PDE=∠PED=30°.
∴∠AED=90°.
∵AD=2,
∴DE=![]() .
.
∵PD=PE, EQ=DQ,
∴PQ是DE的中垂线,
∴PQ= AB=2.
∴![]() =
=![]() .
.
(3)①当QP=QE时,如图1,
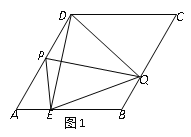
∵∠EQP=∠DQP=30°,
∴∠QPE=∠QEP=∠PDQ =75°.
∴∠PED=∠PDE=15°,
∴∠APE=30°,
∴∠AEP=90°.
∴AP=2AE,PE=PD=![]() AE,
AE,
∴![]() AE+2AE=2,
AE+2AE=2,
∴AE=![]() .
.
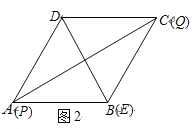
②当PE=QE时,
∵△DEQ是正三角形,
∴△PDE是正三角形,∠ADE=60°,
点E
∴AE=2.
③当PE=PQ时,
∵∠EQP=30°,
∴∠PEQ=30°,由图可知∠PEQ≥60°,
∴点E不存在.
综上所述,当AE为![]() 或2时,△PEQ是等腰三角形.
或2时,△PEQ是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
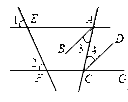
证明:∵ ∠1="∠2" ( 已知 )
∴ AE∥ ( )
∴ ∠EAC =∠ ,( )
而AB平分∠EAC,CD平分∠ACG( 已知 )
∴∠ =![]() ∠EAC,∠4=
∠EAC,∠4=![]() ∠ ( 角平分线的定义 )
∠ ( 角平分线的定义 )
∴∠ =∠4(等量代换)
∴AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市绿化部门决定利用现有的不同种类花卉搭配园艺造型,摆放于城区主要大道的两侧.A、B两种园艺造型均需用到杜鹃花,A种造型每个需用杜鹃花25盆,B种造型每个需用杜鹃花35盆,解答下列问题:
(1)已知人民大道两侧搭配的A、B两种园艺造型共60个,恰好用了1700盆杜鹃花,A、B两种园艺造型各搭配了多少个?
(2)如果搭配一个A种造型的成本W与造型个数![]() 的关系式为:W=100―
的关系式为:W=100―![]() x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数6,
点表示数6,
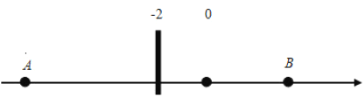
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点![]() ,它表示的数是
,它表示的数是![]() ,则
,则![]() 的最小值是_________;
的最小值是_________;
(3)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数是_________;
点表示的数是_________;
(4)若在原点![]() 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点![]() 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点![]() 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为![]() 秒,请用
秒,请用![]() 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=60°,∠AOC=40°,求∠DOE的度数;
(2)若∠DOE=n°,求∠AOB的度数;
(3)若∠DOE+∠AOB=180°,求∠AOB与∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)每副乒乓球拍和羽毛球拍的单价各是多少元?
(2)若学校购买5副乒乓球拍和3副羽毛球拍,一共应支出多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com