
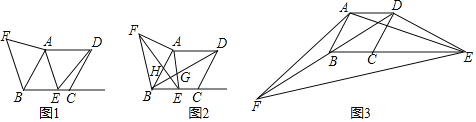
����Ŀ����ͼ1��������ABCD�У���BAD��120����AB��4cm������E������BC�������˶������˶��ٶ�Ϊ1cm/s���˶�ʱ��Ϊts������AE�������߶�AE�Ƶ�A˳ʱ����ת120����AF������BF��
��1����˵������tΪ��ֵ����ABF�����ʼ��Ϊ��ֵ��������ö�ֵ��
��2����ͼ2������EF��BD�����ڵ�H��BD��AE���ڵ�G����tΪ��ֵʱ����HEGΪֱ�������Σ�
��3����ͼ3����F��B��D���㹲��ʱ����tan��FEB��ֵ��
���𰸡���1�������������2���ٵ���HGE��90��ʱ����E���C�غϣ���ʱt��4���ڵ���GHE��90��ʱ��t��2����3��![]()
��������
��1����SAS֤����ABF�ա�ADE����AD��BC�ó�����E��AD�ľ���ʼ�ղ��䣬�ó�S��ADE�Ǹ���ֵ���������������ʽ���ɵó������
��2���ɵ��������ε����ʺ��������ڽǺͶ����ó���AEF��30����
�ٵ���HGE��90��ʱ����E���C�غϣ���ʱt��4��
�ڵ���GHE��90��ʱ��֤��AE��BC����Rt��ABE�У�AB��4cm����ABE��60������ֱ�������ε����ʵó�BE��![]() AB��2cm����ʱt��2��
AB��2cm����ʱt��2��
��3��֤����AFB����FEB������AC��BD�ڵ�O�������ε����ʵó���AOB��90������Rt��ABO�У�AB��4����ABO��30������ֱ�������ε����ʵó�AO��2��BO��2![]() �����FB��4
�����FB��4![]() ���ó�FO��FB+BO��6
���ó�FO��FB+BO��6![]() �������Ǻ������弴�ɵó������
�������Ǻ������弴�ɵó������
��1��֤�����ߡ�BAD����EAF��120����
���BAD����BAE����EAF����BAE��
���FAB����EAD��
���ı���ABCD�����Σ�
��AB��AD��
����ABF����ADE��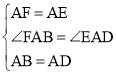 ��
��
���ABF�ա�ADE��SAS����
��AD��BC��
�ද��E��AD�ľ���ʼ�ղ��䣬
��S��ADE�Ǹ���ֵ��
��S��ABF��S��ADE��![]() ��4��4��sin60����
��4��4��sin60����![]() ��4��2
��4��2![]() ��4
��4![]() ��cm2��
��cm2��
��2���⣺��AE��AF����EAF��120����
���AEF��30����
�ٵ���HGE��90��ʱ����E���C�غϣ�
��ʱt��4��
�ڵ���GHE��90��ʱ��
�ߡ�AEF��30����
���HGE��60����
���ı���ABCDΪ���Σ���BAD��120����
���GBE��30����
���GEB��90����
��AE��BC��
��Rt��ABE��AB��4cm����ABE��60����
��BE��![]() AB��2cm��
AB��2cm��
��ʱt��2��
��3���⣺��AF��AE����EAF��120����
���BFE+��AFB��30����
�ߡ�FBE��150����
���BFE+��FEB��30����
���AFB����FEB��
����AC��BD�ڵ�O����ͼ3��ʾ��
���ı���ABCD�����Σ�
��AC��BD��
���AOB��90����
��Rt��ABO��AB��4����ABO��30����
��AO��![]() AB��2��BO��2
AB��2��BO��2![]() ��
��
��![]() FB��AO��4
FB��AO��4![]() ��
��
��FB��4![]() ��
��
��FO��FB+BO��6![]() ��
��
��tan��FEB��tan��AFB��![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
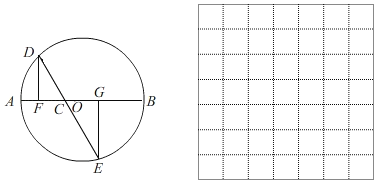
����Ŀ����ͼ��AB����O��ֱ����AB=4cm��CΪAB��һ���㣬����C��ֱ�߽���O��D��E���㣬�ҡ�ACD=60�㣬DF��AB�ڵ�F��EG��AB�ڵ�G������C��AB���˶�ʱ����AF=xcm��DE=ycm(��x��ֵΪ0��3ʱ��y��ֵΪ2)��̽������y���Ա���x�ı仯���仯�Ĺ��ɣ�
��1��ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ����Ӧֵ�����±���
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
��2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��3����ϻ����ĺ���ͼ������⣺��F���O�غ�ʱ��DE����ԼΪ��������cm(�������һλС��)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ķ���
�ķ���![]() .
.
��1����֤������![]() Ϊ�κ�ʵ�����˷�������ʵ������
Ϊ�κ�ʵ�����˷�������ʵ������
��2����������![]() ��
��![]() �ύ��������ͬ�������㣬��
�ύ��������ͬ�������㣬��![]() Ϊ����������ȷ���������ߵĽ���ʽ��
Ϊ����������ȷ���������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������ϵ�������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ������ֵ
������ֵ![]() ����Сֵ��
����Сֵ��![]() ��
��
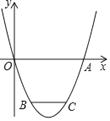
��1���������ߵĽ���ʽ��
��2����![]() Ϊ�������ϵĵ㣬���ڶԳ������࣮��
Ϊ�������ϵĵ㣬���ڶԳ������࣮��![]() �ύ�������ڵ�
�ύ�������ڵ�![]() ������
������![]() ��
��![]() ����
����![]() ��
��
����![]() ��ֵ��
��ֵ��
������![]() ���߶�
���߶�![]() �ϣ��Ե�
�ϣ��Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ����
Ϊ�뾶��Բ����![]() ��
��![]() ��һ������ʱ�����
��һ������ʱ�����![]() �ĺ����꣮
�ĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
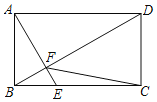
����Ŀ����ͼ���ھ���ABCD�У���E��BC���ϵ�һ�㣬��AE��BD������Ϊ��F����DAE��2��BAE��
��1����֤��BF��DF��1��3��
��2�����ı���EFDC�����Ϊ11������CEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
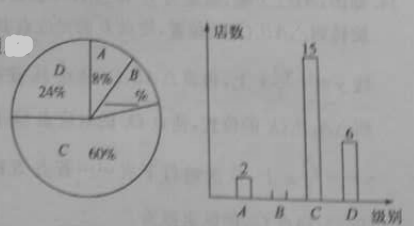
����Ŀ��Ϊ���ƽ������˶��ķ�չ��ijУ��֯У�������˶��ᣬ����������������ë��ƹ�������Ҫ��ÿλѧ������μ�һ���ֻ�ܲμ�һ�ij����һ��ѧ�������Լ��˽�İ��������������ͼ��ʾ�IJ�����ͳ�Ʊ�������ͳ��ͼ.

�����ͼ�����ṩ����Ϣ������������⣺
��1��ͼ����m=________��n=________��
��2������Уѧ������1000�ˣ����У�μ���ë��������ԼΪ________�ˣ�
��3���ð�μ�ƹ������4λͬѧ�У���3λ��ͬѧ���ֱ���A��B��C��ʾ����1λŮͬѧ����D��ʾ������������ѡ������ͬѧ�μ�˫�����������״ͼ���б������ǡ��ѡ��һ��һŮ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������5�£�ij������ҵ���������ȡ�����IJ�����ҵ�������������������ȡ�ĸ���ҵ�����갴�������ɼ��ֳ���![]() ��
��![]() ��
��![]() ��
��![]() �ĸ��ȼ��������������²�����������ͳ��ͼ������ͳ��ͼ.
�ĸ��ȼ��������������²�����������ͳ��ͼ������ͳ��ͼ.
����������Ϣ������������⣺
��1���������������ȡ�˶��ټ���ҵ�����ꣿ
��2���벹����������ͳ��ͼ������ͳ��ͼ������ͼ�б�ע��Ӧ���ݣ�
��3����![]() ��
��![]() �����ȼ�����ҵ����������ѡ2�ҽ���Ӫ�����飬������������һ����
�����ȼ�����ҵ����������ѡ2�ҽ���Ӫ�����飬������������һ����![]() �ȼ��ĸ���.
�ȼ��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ij�¶Ȳ���������£�ͨ��һ����һ�εض��������Ļ�����ѹ�����ÿһ�μ�ѹ����������������![]() ����������ױڲ�����ѹǿ
����������ױڲ�����ѹǿ![]() �Ĺ�ϵ��������ͼ��ʾ�ĺ���ͼ����б�ʾ������˵����ȷ���ǣ� ��
�Ĺ�ϵ��������ͼ��ʾ�ĺ���ͼ����б�ʾ������˵����ȷ���ǣ� ��
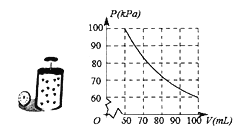
A.��ѹP�����V�Ĺ�ϵʽΪ![]()
B.����ѹ![]() ʱ�����V��ȡֵ��ΧΪ
ʱ�����V��ȡֵ��ΧΪ![]()
C.�����V��Ϊԭ����һ��ʱ����Ӧ����ѹPҲ��Ϊԭ����һ��
D.��![]() ʱ����ѹP�������V���������С
ʱ����ѹP�������V���������С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
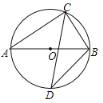
����Ŀ����ͼ��ABΪ��O��ֱ����CΪԲ�ϣ���A��B�⣩һ���㣬��ACB�Ľ�ƽ���߽���O��D����AC=8��BC=6����BD�ij�Ϊ______.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com