
【题目】如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5![]() ,且
,且![]() ,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=-
,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=-![]() +c经过点E,且与AB边相交于点F.
+c经过点E,且与AB边相交于点F.

(1)求证:△ABD∽△ODE;
(2)若M是BE的中点,连接MF,求证:MF⊥BD;
(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.
【答案】(1)见解析;(2)见解析;(3)(﹣4,0)或(12,0)
【解析】
试题由折叠和矩形的性质可知∠EDB=∠BCE=90°,可证得∠EDO=∠DBA,可证明△ABD∽△ODE;由条件可求得OD、OE的长,可求得抛物线解析式,结合(1)由相似三角形的性质可求得DA、AB,可求得F点坐标,可得到BF=DF,又由直角三角形的性质可得MD=MB,可证得MF为线段BD的垂直平分线,可证得结论;过D作x轴的垂线交BC于点G,设抛物线与x轴的两个交点分别为M、N,可求得DM=DN=DG,可知点M、N为满足条件的点Q,可求得Q点坐标.
试题解析:(1)证明:∵四边形ABCO为矩形,且由折叠的性质可知△BCE≌△BDE,
∴∠BDE=∠BCE=90°,∵∠BAD=90°,∴∠EDO+∠BDA=∠BDA+∠DAB=90°,
∴∠EDO=∠DBA,且∠EOD=∠BAD=90°,∴△ABD∽△ODE;
(2)证明:∵![]() ,∴设OD=4x,OE=3x,则DE=5x,∴CE=DE=5x,∴AB=OC=CE+OE=8x,
,∴设OD=4x,OE=3x,则DE=5x,∴CE=DE=5x,∴AB=OC=CE+OE=8x,
又∵△ABD∽△ODE,∴![]() ,∴DA=6x,∴BC=OA=10x,
,∴DA=6x,∴BC=OA=10x,
在Rt△BCE中,由勾股定理可得![]() ,即
,即![]() ,解得x=1,
,解得x=1,
∴OE=3,OD=4,DA=6,AB=8,OA=10,∴抛物线解析式为y=﹣![]() +3,
+3,
当x=10时,代入可得y=![]() ,∴AF=
,∴AF=![]() ,BF=AB﹣AF=8﹣
,BF=AB﹣AF=8﹣![]() =
=![]() ,
,
在Rt△AFD中,由勾股定理可得DF=![]() ∴BF=DF,
∴BF=DF,
又M为Rt△BDE斜边上的中点,∴MD=MB,∴MF为线段BD的垂直平分线,∴MF⊥BD;
(3)解:由(2)可知抛物线解析式为y=﹣![]() +3,设抛物线与x轴的两个交点为M、N,
+3,设抛物线与x轴的两个交点为M、N,
令y=0,可得0=﹣![]() +3,解得x=﹣4或x=12,∴M(﹣4,0),N(12,0),
+3,解得x=﹣4或x=12,∴M(﹣4,0),N(12,0),
过D作DG⊥BC于点G,如图所示,
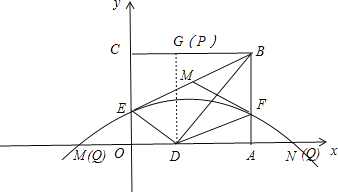
则DG=DM=DN=8,∴点M、N即为满足条件的Q点,
∴存在满足条件的Q点,其坐标为(﹣4,0)或(12,0


科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数y=![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适逢中高考期间,某文具店平均每天可卖出![]() 支
支![]() 铅笔,卖出
铅笔,卖出![]() 支铅笔的利润是
支铅笔的利润是![]() 元,经调查发现,零售单价毎降
元,经调查发现,零售单价毎降![]() 元,每天可多卖出
元,每天可多卖出![]() 支铅笔,为了使每天获取的利润更多,该文具店决定把零售单价下降
支铅笔,为了使每天获取的利润更多,该文具店决定把零售单价下降![]() 元
元![]()
![]() 零售单价下降
零售单价下降![]() 元后,该文具店平均每天可卖出________支铅笔,总利润为________元.
元后,该文具店平均每天可卖出________支铅笔,总利润为________元.
![]() 在不考虑其他因素的条件下,当
在不考虑其他因素的条件下,当![]() 定为多少元时,才能使该文具店每天卖
定为多少元时,才能使该文具店每天卖![]() 铅笔获取的利润为
铅笔获取的利润为![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图![]() ,
,![]() .
.
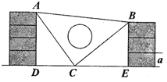
(1)求证:![]() ;
;
(2)若三角板的一条直角边![]() ,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).
,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
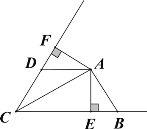
【题目】如图,AC平分∠BCD,AB=AD, AE⊥BC于E,AF⊥CD于F
(1)若∠ABE= 50° ,求∠CDA的度数.
(2)若AE=4,BE=2,CD=6,求四边形AECD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲车从A地到B地,乙车从B地到A地,乙车先出发先到达,甲乙两车之间的距离y(千米)与行驶的时间x(小时)的函数关系如图所示,则下列说法中不正确的是( )
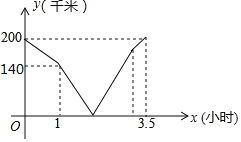
A.甲车的速度是80km/hB.乙车的速度是60km/h
C.甲车出发1h与乙车相遇D.乙车到达目的地时甲车离 B地10km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com