
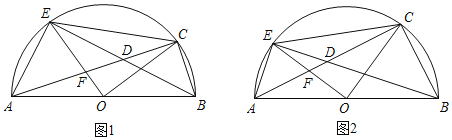
【题目】如图,AB是半圆O的直径,C为半圆弧上一点,在AC上取一点D,使BC=CD,连结BD并延长交⊙O于E,连结AE,OE交AC于F.
(1)求证:△AED是等腰直角三角形;
(2)如图1,已知⊙O的半径为![]() .
.
①求![]() 的长;
的长;
②若D为EB中点,求BC的长.
(3)如图2,若AF:FD=7:3,且BC=4,求⊙O的半径.
【答案】(1)见解析;(2)①![]() ;②
;②![]() ;(3)
;(3)![]()
【解析】
(1)由已知可得△BCD是等腰直角三角形,所以∠CBD=∠EAD=45°,因为∠AEB=90°可证△AED是等腰直角三角形;
(2)①已知可得∠EAD=45°,∠EOC=90°,则△EOC是等腰直角三角形,所以CE的弧长=![]() ×2×π×
×2×π×![]() =
=![]() ;
;
②由已知可得ED=BD,在Rt△ABE中,(2![]() )2=AE2+(2AE)2,所以AE=2,AD=2
)2=AE2+(2AE)2,所以AE=2,AD=2![]() ,易证△AED∽△BCD,所以BC=
,易证△AED∽△BCD,所以BC=![]() ;
;
(3)由已知可得AF=![]() AD,过点E作EG⊥AD于G,EG=
AD,过点E作EG⊥AD于G,EG=![]() AD,GF=
AD,GF=![]() AD,tan∠EFG=
AD,tan∠EFG=![]() ,得出FO=
,得出FO=![]() r,在Rt△COF中,FC=
r,在Rt△COF中,FC=![]() r,EF=
r,EF=![]() r,在Rr△EFG中,由勾股定理,求出AD=
r,在Rr△EFG中,由勾股定理,求出AD=![]() r,AF=
r,AF=![]() r,所以AC=AF+FC=
r,所以AC=AF+FC=![]() ,CD=BC=4,AC=4+AD,可得
,CD=BC=4,AC=4+AD,可得![]() r=4+
r=4+![]() r,解出r即可.
r,解出r即可.
解:(1)∵BC=CD,AB是直径,
∴△BCD是等腰直角三角形,
∴∠CBD=45°,
∵∠CBD=∠EAD=45°,
∵∠AEB=90°,
∴△AED是等腰直角三角形;
(2)①∵∠EAD=45°,
∴∠EOC=90°,
∴△EOC是等腰直角三角形,
∵⊙O的半径为![]() ,
,
∴CE的弧长=![]() ×2×π×
×2×π×![]() =
=![]() ,
,
故答案为:![]() ;
;
②∵D为EB中点,
∴ED=BD,
∵AE=ED,
在Rt△ABE中,(2![]() )2=AE2+(2AE)2,
)2=AE2+(2AE)2,
∴AE=2,
∴AD=2![]() ,
,
∵ED=AE,CD=BC,∠AED=∠BCD=90°,
∴△AED∽△BCD,
∴BC=![]() ,
,
故答案为:![]() ;
;
(3)∵AF:FD=7:3,
∴AF=![]() AD,
AD,
过点E作EG⊥AD于G,
∴EG=![]() AD,
AD,
∴GF=![]() AD,
AD,
∴tan∠EFG=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴FO=![]() r,
r,
在Rt△COF中,FC=![]() r,
r,
∴EF=![]() r,
r,
在Rt△EFG中,(![]() r)2=(
r)2=(![]() AD)2+(
AD)2+(![]() AD)2,
AD)2,
∴AD=![]() r,
r,
∴AF=![]() r,
r,
∴AC=AF+FC=![]() r,
r,
∵CD=BC=4,
∴AC=4+AD=4+![]() r,
r,
∴![]() r=4+
r=4+![]() r,
r,
∴r=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)求证:四边形CDBF是平行四边形;
(2)若∠FDB=30°,∠ABC=45°,BC=4![]() ,求DF的长.
,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏省第十九届运动会将于2018年9月在扬州举行开幕式,某校为了了解学生“最喜爱的省运会项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”、“游泳”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的省运会项目的人数调查统计表


根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 ,![]() ;
;
(2)扇形统计图中“自行车”对应的扇形的圆心角为 度;
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
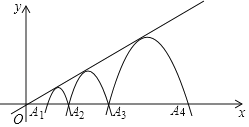
【题目】若二次函数的图象与x轴的两个交点和顶点构成等边三角形,则称这样的二次函数的图象为标准抛物线.如图,自左至右的一组二次函数的图象T1,T2,T3……是标准抛物线,且顶点都在直线y=![]() x上,T1与x轴交于点A1(2,0),A2(A2在A1右侧),T2与x轴交于点A2,A3,T3与x轴交于点A3,A4,……,则抛物线Tn的函数表达式为_____.
x上,T1与x轴交于点A1(2,0),A2(A2在A1右侧),T2与x轴交于点A2,A3,T3与x轴交于点A3,A4,……,则抛物线Tn的函数表达式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,AE 是∠BAC 的平分线,∠ABC 的平分线 BM 交 AE 于点 M,点 O在 AB 上,以点O 为圆心,OB 的长为半径的圆经过点 M,交 BC 于点G,交 AB 于点 F.
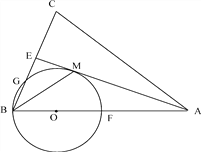
(1)求证:AE 为⊙O 的切线.
(2)当 BC=8,AC=12 时,求⊙O 的半径.
(3)在(2)的条件下,求线段 BG 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
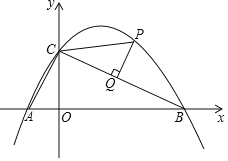
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴相交于点A(-1,0),B(4,0),与
轴相交于点A(-1,0),B(4,0),与![]() 轴相交于点C.
轴相交于点C.
(1)求该函数的表达式;
(2)若点P(2,m)为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC,求线段PQ的长;
(3)在(2)的条件下,点M为该函数图象上一点,且∠MAP=45°,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c为正数,若关于x的一元二次方程ax2+bx+c=0有两个实数根,则关于x的方程a2x2+b2x+c2=0解的情况为( )
A.有两个不相等的正根B.有一个正根,一个负根
C.有两个不相等的负根D.不一定有实数根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com