
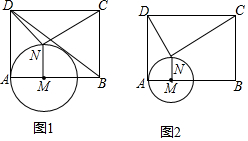
分析 (1)①判断出△BME∽△BDA,得出比例式建立方程求解即可得出结论;
②先求出MN,CD边上的高,用三角形的面积公式即可得出结论;
(2)先判断出△DFN∽△NGC,得出比例式求出时间t,最后,求出MN,判断是否满足题意.
解答 (1)①如图1, 设⊙M切BD于点E,连接ME,则ME⊥BD,
设⊙M切BD于点E,连接ME,则ME⊥BD,
∴∠BME=∠BAD=90°,
∵∠MBE=∠DBA,
∴△BME∽△BDA,
∴$\frac{BM}{BD}=\frac{ME}{DA}$,
即$\frac{12-2t}{\sqrt{81+144}}=\frac{2t}{9}$,
解之,得t=$\frac{9}{4}$
②∵MN=AM=2t=$\frac{9}{2}$,
∴CD边上的高为AD-MN=9-$\frac{9}{2}$=$\frac{9}{2}$,
∴S△CDN=$\frac{1}{2}$×12×$\frac{9}{2}$=27.
(2)如图2,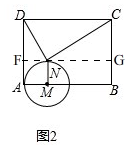 过点N作直线FG⊥MN,分别交AD、BC于点F、G.
过点N作直线FG⊥MN,分别交AD、BC于点F、G.
则FN=2t,GN=12-2t,DF=CG=9-2t,
∵∠CND=90°,
∴∠DNF+∠CNG=90°,
∵∠DNF+∠FDN=90°,
∴∠FDN=∠CNG,
∵∠DFN=∠NGC=90°
∴△DFN∽△NGC,
∴$\frac{DF}{NG}=\frac{FN}{GC}$,
∴$\frac{9-2t}{12-2t}=\frac{2t}{9-2t}$,
∴8t2-60t+81=0,
∴t=$\frac{15±3\sqrt{7}}{4}$,
当t=$\frac{15+3\sqrt{7}}{4}$时,MN=2t=$\frac{15+3\sqrt{7}}{2}$>9,
∴点N在矩形ABCD外,不合题意,舍去;
当t=$\frac{15-3\sqrt{7}}{4}$时,MN=2t=$\frac{15-3\sqrt{7}}{2}$<9,
∴点N在矩形ABCD内,符合题意,
∴t=$\frac{15-3\sqrt{7}}{4}$.
点评 此题是圆的综合题,主要考查了圆的切线的性质,相似三角形的判定和性质,矩形的性质,解(1)的关键是判断出△BME∽△BDA,解(2)的关键是判断出△DFN∽△NGC,是一道中等难度的题目.


科目:初中数学 来源:2016~2017学年安徽省芜湖市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
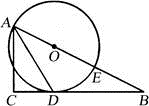
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=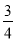 ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
估算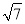 的值是( )
的值是( )
A. 在1和2之间 B. 在2和3之间
C. 在3和4之间 D. 在4和5之间
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
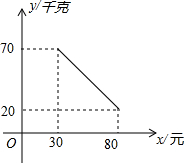 某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80.
某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com