

分析 (1)根据梯形的面积公式即可得出结论;
(2)根据平行四边形的对边相等DQ=PC建立方程求解即可得出结论;
(3)分两种情况①利用等腰三角形的三线合一的性质得出QE=$\frac{1}{2}$QD,再用矩形的对边相等建立方程求解即可;
②利用勾股定理建立方程即可得出结论.
解答 解:(1)由题意得∵AQ=tcm,BP=2t cm,
∴当四边形ABPQ的面积为18cm2时
∴$\frac{1}{2}$(t+2t)×6=18,
解得t=2;
所以,t=2s时,四边形ABPQ的面积为18cm2;
(2)由题意得∵AQ=tcm,BP=2t cm,
∵AD=8cm,BC=10cm
∴DQ=(8-t)cm,PC=(10-2t)cm,
∵四边形PCDQ是平行四边形,
∴DQ=PC
∴8-t=10-2t,
解得t=2;
综上所述,以P、Q、C、D为顶点的四边形是平行四边形,t的值是2;
(3)①如图①,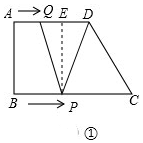 若PQ=PD,过P作PE⊥AD于E,
若PQ=PD,过P作PE⊥AD于E,
则QD=8-t,
∴QE=$\frac{1}{2}$QD=$\frac{1}{2}$(8-t),
∴AE=AQ+QE=t+$\frac{1}{2}$(8-t)=$\frac{1}{2}$(8+t),
∵易证四边形ABPE是矩形,
∴AE=BP,
∴$\frac{1}{2}$(8+t)=2t,
解得t=$\frac{8}{3}$
②如图②,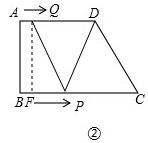 若QD=QP,过Q作QF⊥BC于F,
若QD=QP,过Q作QF⊥BC于F,
则QF=6,FP=2t-t=t,
在Rt△QPF中,由勾股定理得:QF2+FP2=QP2,
即62+t2=(8-t)2,
解得t=$\frac{7}{4}$
综上所述,当t=$\frac{8}{3}$或$\frac{7}{4}$.
点评 此题是四边形综合题,主要考查了梯形的面积公式,平行四边形的性质,矩形的性质,勾股定理,解不同的关键是用方程的思想解决问题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.715×104 | B. | 0.715×10-4 | C. | 7.15×105 | D. | 7.15×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x$>\frac{3}{2}$ | B. | x$≥\frac{3}{2}$ | C. | x$<\frac{3}{2}$ | D. | x$≤\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
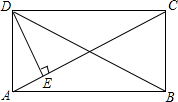 已知:如图,在矩形ABCD中,DE⊥AC于点E,∠ADE:∠CDE=1:2,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC于点E,∠ADE:∠CDE=1:2,那么∠BDC等于( )| A. | 60° | B. | 45° | C. | 22.5° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com