
分析 二次三项式是完全平方式,则常数项是一次项系数一半的平方,根据此方法分别求解.
解答 解:(1)x2+6x+9=(x+3)2;
(2)x2-x+$\frac{1}{4}$=(x-$\frac{1}{2}$)2;
(3)4x2+4x+1=(2x+1)2;
(4)x2-$\frac{2}{5}$x+$\frac{1}{25}$=(x-$\frac{1}{5}$)2.
故答案为9,3;$\frac{1}{4}$,$\frac{1}{2}$;1,1;$\frac{1}{25}$,$\frac{1}{5}$.
点评 本题考查了配方法的应用:用配方法解一元二次方程;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.本题的关键是二次三项式是完全平方式,则常数项是一次项系数一半的平方.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
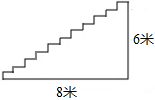 如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?
如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF
如图,已知点E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
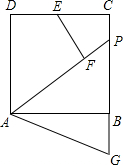 如图,P为正方形ABCD边BC上一点,F在AP上,且AF=AD,EF⊥AP交CD于点E,G为CB延长线上一点,BG=DE.
如图,P为正方形ABCD边BC上一点,F在AP上,且AF=AD,EF⊥AP交CD于点E,G为CB延长线上一点,BG=DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com