
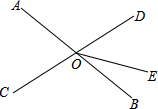
 如图,直线AB,CD相交于O,已知∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE.
如图,直线AB,CD相交于O,已知∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE. 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 一班 | a | b | 90 |
| 二班 | 87.6 | 80 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:
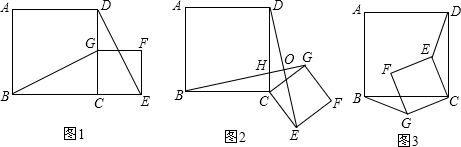
 如图,在△ABC中,已知∠BAC=45°,AD⊥BC于点D,BD=2,DC=3,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题:
如图,在△ABC中,已知∠BAC=45°,AD⊥BC于点D,BD=2,DC=3,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
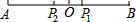 如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项.
如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com