
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
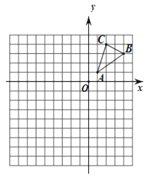
(1)请作出![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 的
的![]() ;
;
(2)以点![]() 为位似中心,将
为位似中心,将![]() 扩大为原来的2倍,得到
扩大为原来的2倍,得到![]() ,请在
,请在![]() 轴的左侧画出
轴的左侧画出![]() ;
;
(3)请直接写出![]() 的正弦值.
的正弦值.
【答案】(1)答案见解析;(2)答案见解析;(3)![]() .
.
【解析】
(1)先根据点坐标旋转的规律得出点![]() 的坐标,再在直角坐标系中描点,然后顺次连接即可得;
的坐标,再在直角坐标系中描点,然后顺次连接即可得;
(2)先根据位似的定义得出点![]() 的坐标,再在直角坐标系中描点,然后顺次连接即可得;
的坐标,再在直角坐标系中描点,然后顺次连接即可得;
(3)先利用“补”的数学思想求出![]() 的面积,再利用两点之间的距离公式分别求出AB、BC的长,然后利用三角形的面积公式可求出AB边上的高,最后根据正弦的定义即可得.
的面积,再利用两点之间的距离公式分别求出AB、BC的长,然后利用三角形的面积公式可求出AB边上的高,最后根据正弦的定义即可得.
(1)在直角坐标系中,点绕原点O逆时针旋转![]() 的坐标变换规律为:先将横、纵坐标的位置互换,再将横坐标变为相反数
的坐标变换规律为:先将横、纵坐标的位置互换,再将横坐标变为相反数
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
再在直角坐标系中描点,然后顺次连接即可得![]() ,如图所示:
,如图所示:
(2)以点![]() 为位似中心,将
为位似中心,将![]() 扩大为原来的2倍,且点
扩大为原来的2倍,且点![]() 在y轴的左侧
在y轴的左侧
则![]() ,
,![]() ,
,![]()
即![]() ,
,![]() ,
,![]()
再在直角坐标系中描点,然后顺次连接即可得![]() ,如图所示:
,如图所示:
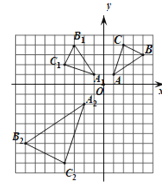
(3)由题意得:![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
设AB边上的高为![]()
则![]() ,即
,即![]()
解得![]()
![]()
即![]() 的正弦值为
的正弦值为![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
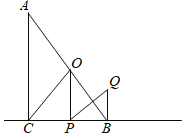
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与B、C重合),连接OC、OP,将OP绕点P顺时针旋转60°,得到线段PQ,连接BQ,若∠BPO=15°,BP=4,则BQ的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
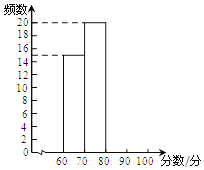
【题目】某学校组织七年级学生进行“垃圾分类”知识测试,现随机抽取部分学生的成绩进行统计,并绘制如下频数分布表以及频数分布直方图.
分数档 | 分数段/分 | 频数 | 频率 |
A | 90<x≤100 | a | 0.12 |
B | 80<x≤90 | b | 0.18 |
C | 70<x≤80 | 20 | c |
D | 60<x≤70 | 15 | d |
请根据以上信息,解答下列问题:
(1)已知A,B档的学生人数之和等于D档学生人数,求被抽取的学生人数,并把频数分布直方图补充完整.
(2)该校七年级共有200名学生参加测试,请估计七年级成绩在C档的学生人数.
(3)你能确定被抽取的这些学生的成绩的众数在哪一档吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某跳高集训队,对集训队员进行了一次跳高测试,经过统计,将集训队员的测试成绩(单位:m),绘制成尚不完整的扇形统计图(图①)与条形统计图(图②).
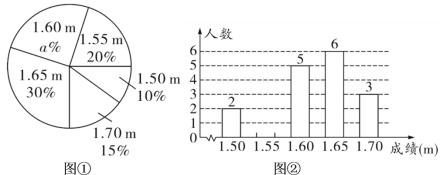
(1)![]() ________,请将条形统计图补充完整;
________,请将条形统计图补充完整;
(2)求集训队员测试成绩的众数;
(3)教练发现,测试成绩不包括两名请假的队员,补测后,把这两名队员的成绩(均是0.05的整数倍)与原测试成绩并成一组新数据,求新数据的中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
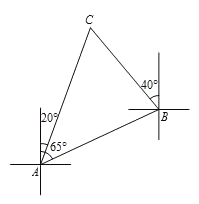
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,其中
两点,其中![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() ,连接
,连接![]() .
.
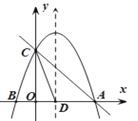
(1)求抛物线和直线![]() 的解析式:
的解析式:
(2)若抛物线上存在一点![]() ,使
,使![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标;
的坐标;
(3)在抛物线的对称轴上是否存在一点![]() ,使线段
,使线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到线段
得到线段![]() ,且
,且![]() 恰好落在抛物线上?若存在,求出点
恰好落在抛物线上?若存在,求出点![]() 的坐标;若不存在,请说叫理由.
的坐标;若不存在,请说叫理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽从学校去图书馆,小红沿同一条路从图书馆回学校,她们同时出发,小丽开始跑步中途改为步行,到达图书馆恰好用30分钟,小红骑自行车回学校,两人离学校的路程![]() 与各自离开出发地的时间(分钟)之间的函数图象如图所示.
与各自离开出发地的时间(分钟)之间的函数图象如图所示.
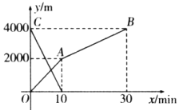
(1)小红骑自行车的速度是_____米/分钟,小丽从学校到图书馆的平均速度是_____米/分钟;
(2)求小丽从学校去图书馆时,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)两人出发后多少分钟相遇,相遇地点离图书馆的路程是多少米.(结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
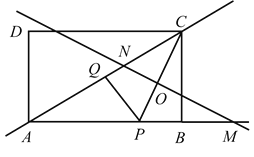
【题目】如图,矩形![]() 中,AB=8,BC=6,点
中,AB=8,BC=6,点![]() 是射线
是射线![]() 上一动点,设
上一动点,设![]() .过点
.过点![]() 做射线
做射线![]() 的垂线段
的垂线段![]() ,垂足为
,垂足为![]() ,作
,作![]() 的垂直平分线
的垂直平分线![]() 交射线
交射线![]() 于点
于点![]() ,交直线
,交直线![]() 于
于![]() .
.
![]() 点
点![]() 在边
在边![]() 上时.①用含
上时.①用含![]() 的代数式表示
的代数式表示![]() .②当
.②当![]() 时,直线ON交射线CD于
时,直线ON交射线CD于![]() ,求CE的长.
,求CE的长.
![]() 当
当![]() 为何值时,过
为何值时,过![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切.
相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
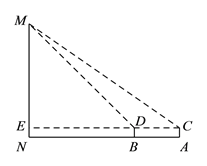
【题目】在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com