
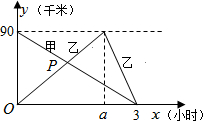
 在一条笔直的公路上有A、B两地,甲从A地去B地,乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,如图是甲、乙两人离B地的距离y(千米)和时间x(小时)之间的函数图象.请根据图象回答下列问题:
在一条笔直的公路上有A、B两地,甲从A地去B地,乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,如图是甲、乙两人离B地的距离y(千米)和时间x(小时)之间的函数图象.请根据图象回答下列问题:分析 (1)观察函数图象即可得出A、B两地的距离,由乙往返需要3小时结合返回时的速度是原来的2倍,即可求出a值;
(2)观察函数图象找出点的坐标,利用待定系数法求出甲、乙离B地的距离y和时间x之间的函数关系式,令两函数关系式相等即可求出点P的坐标,再解释出它的实际意义即可;
(3)分0≤x<1.2、1.2≤x<2和2≤x≤3三段,找出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)观察函数图象可知:A、B两地的距离是90千米,
∵乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,
∴a=3×$\frac{2}{2+1}$=2.
故答案为:90;2.
(2)设甲离B地的距离y(千米)和时间x(小时)之间的函数关系式为y=kx+b,乙离B地的距离y(千米)和时间x(小时)之间的函数关系式为y=mx+n,
将(0,90)、(3,0)代入y=kx+b中,
$\left\{\begin{array}{l}{b=90}\\{3k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-30}\\{b=90}\end{array}\right.$,
∴甲离B地的距离y和时间x之间的函数关系式为y=-30+90;
将(0,0)、(2,90)代入y=mx+n中,
$\left\{\begin{array}{l}{n=0}\\{2m+n=90}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=45}\\{n=0}\end{array}\right.$,
∴此时y=45x(0≤x≤2);
将(2,90)、(3,0)代入y=mx+n中,
$\left\{\begin{array}{l}{2m+n=90}\\{3m+n=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-90}\\{n=270}\end{array}\right.$,
此时y=-90x+270(2≤x≤3).
∴乙离B地的距离y和时间x之间的函数关系式为y=$\left\{\begin{array}{l}{45x(0≤x≤2)}\\{-90x+270(2≤x≤3)}\end{array}\right.$.
令y=-30+90=45x,解得:x=1.2,
当x=1.2时,y=45x=45×1.2=54,
∴点P的坐标为(1.2,54).
点P的实际意义是:甲、乙分别从A、B两地出发,经过1.2小时相遇,这时离B地的距离为54千米.
(3)当0≤x<1.2时,-30x+90-45x=15,
解得:x=1;
当1.2≤x<2时,45x-(-30x+90)=15,
解得:x=1.4;
当2≤x≤3时,-90x+270-(-30x+90)=15,
解得:x=2.75.
综上所述:当x为1、1.4或2.75时,甲乙两人相距15千米.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及解一元一次方程,解题的关键是:(1)观察函数图象找出A、B两地的距离;(2)观察函数图象找出点的坐标,利用待定系数法求出函数关系式;(3)分0≤x<1.2、1.2≤x<2和2≤x≤3三段,找出关于x的一元一次方程.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 造成医患关系紧张的原因(单选) A.药价高 B.检测项目太多且收费太高 C.住院报销比例低 D.医疗费与个人收入不相称 E.其他 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.
某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.| 日人均诵读时间x/h | 人数 | 百分比 |
| 0≤x≤0.5 | 6 | |
| 0.5<x≤1 | 30 | |
| 1<x≤1.5 | 50% | |
| 1.5<x≤2 | 10 | 10% |
| 2<x≤2.5 | b | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)
在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | P′(-1,-2) | B. | P′(1,-2) | C. | P′(-1,2) | D. | P′(1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com