
【题目】如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD. 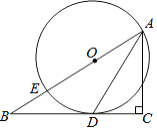
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC= ![]() ,求BD的长.
,求BD的长.
【答案】
(1)解:连接OD.

∵OD、OA是⊙O的半径,
∴OA=OD.
∴∠OAD=∠ODA.
∵点D是⊙O的切点,
∴∠ODC=90°
又∵∠C=90°,
∴OD∥AC.
∴∠ODA=∠DAC,
∴∠OAD=∠CAD,
∴AD平分∠BAC.
(2)解:如图2所示:连接ED.

∵⊙O的半径为5,AE是圆O的直径,
∴AE=10,∠EDA=90°.
∵∠EAD=∠CAD,sin∠DAC= ![]() ,
,
∴AD= ![]() ×10=4
×10=4 ![]() .
.
∴DC= ![]() ×4
×4 ![]() =4,AC=
=4,AC= ![]() ×4
×4 ![]() =8.
=8.
∵OD∥AC,
∴△BOD∽△BAC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:BD= ![]() .
.
【解析】(1)连接OD.先依据平行线的判定定理证明OD∥AC,然后依据平行线的性质和等腰三角形的性质证明∠OAD=∠DAC,于是可证明AD平分∠BAC.(2)连接ED、OD.由题意可知AE=10.接下来,在△ADA中,依据锐角三角函数的定义可求得AD的长,然后在△ADC中,可求得DC和AC的长,由OD∥AC可证明△BOD∽△BAC,然后由相似三角形的性质可列出关于BD的方程.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= ![]() (m≠0)交于点A(2,﹣3)和点B(n,2).
(m≠0)交于点A(2,﹣3)和点B(n,2). 
(1)求直线与双曲线的表达式;
(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= ![]() (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
(m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,请证明:BD=AB﹣AF;
(2)试探索:点D在AB的延长线或反向延长线上时,请在备用图中画出图形,(1)中的结论是否成立?若不成立,请直接写出正确结论(不需要证明).
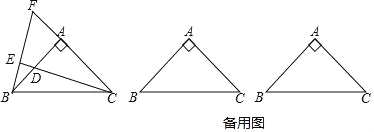
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.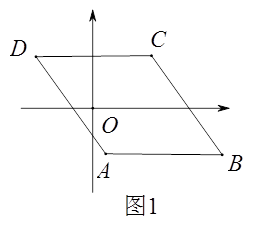

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )

A. 10cm B. 12cm C. 15cm D. 17cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
如图①,在△ABC中,点D、E、F分别在边AB、AC、CB上,且DE∥BC,EF∥AB,若∠ABC=65°,求∠DEF的度数.请将下面的解答过程补充完整,并填空(理由或数学式):
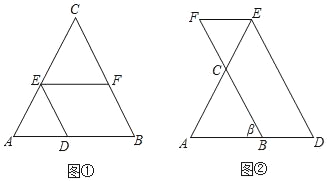
解:∵DE∥BC( )
∴∠DEF= ( )
∵EF∥AB
∴ =∠ABC( )
∴∠DEF=∠ABC( )
∵∠ABC=65°
∴∠DEF=
应用:
如图②,在△ABC中,点D、E、F分别在边AB、AC、BC的延长线上,且DE∥BC,EF∥AB,若∠ABC=β,则∠DEF的大小为 (用含β的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
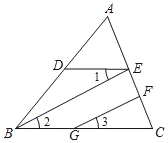
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com