
【题目】有关于![]() ,
,![]() 的方程
的方程![]() .
.
(1)当![]() 和
和![]() 时,所得方程组成的方程组是
时,所得方程组成的方程组是![]() ,它的解是______;
,它的解是______;
(2)当![]() 和
和![]() 时,所得方程组成的方程组是______它的解是______;
时,所得方程组成的方程组是______它的解是______;
(3)猜想:无论![]() 取何值,关于
取何值,关于![]() ,
,![]() 的方程
的方程![]() 一定有一个解是______.
一定有一个解是______.
(4)猜想:无论![]() 取何值,关于
取何值,关于![]() ,
,![]() 的方程
的方程![]() 一定有一个解是______.
一定有一个解是______.
科目:初中数学 来源: 题型:
【题目】一股民上星期五买进某公司股票![]() 股,每股
股,每股![]() 元,下表为本周内每日该股票的涨跌情况(单位:元)
元,下表为本周内每日该股票的涨跌情况(单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
![]() 星期三收盘时,每股是________元;
星期三收盘时,每股是________元;
![]() 本周内每股最高价为________元,每股最低价为________元;
本周内每股最高价为________元,每股最低价为________元;
![]() 已知该股民买进股票时付了
已知该股民买进股票时付了![]() ‰的手续费,卖出时还需付成交额
‰的手续费,卖出时还需付成交额![]() ‰的手续费和
‰的手续费和![]() ‰的交易锐,如果该股民在星期五收盘前将全部股票卖出,他的收益情况如何?
‰的交易锐,如果该股民在星期五收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
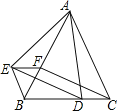
【题目】如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
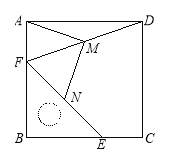
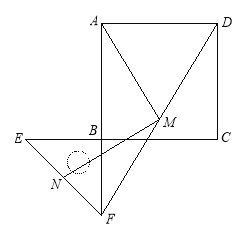
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
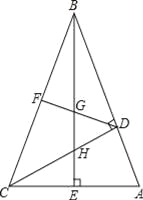
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 180 |
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的大小关系,并证明你的结论。
的大小关系,并证明你的结论。
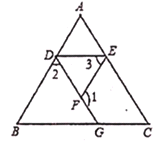
猜想:∠AED=∠C,
理由:∵∠2+∠ADF=180°( ),
∠1+∠2=180°( ),
∴∠1=∠ADF( ),
∴AD∥EF( ),
∴∠3=∠ADE( ),
∵∠3=∠B( ),
∴∠B=∠ADE( ),
∴DE∥BC( ),
∴∠AED=∠C( ),
查看答案和解析>>
科目:初中数学 来源: 题型:
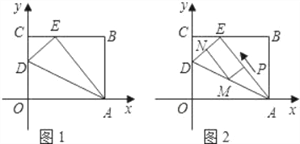
【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com