【题目】如图，在四边形
中，
， 
交
于
，
是的中点，连接
并延长，交
于点
，恰好是的中点.
（1）求
的值；
（2）若
，求证：四边形
是矩形.
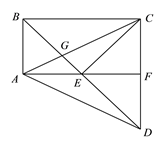
【答案】（1）
（2）证明见解析
【解析】分析: （1）根据AB∥CD，得到∠ABE=∠EDC.证明△ABE∽△FDE.得到
.进一步说明AB=DF.再证明△ABG∽△CDG，
.
根据AB∥CF，AB=CF，证明四边形ABCF是平行四边形. 证明∠CFA=90°.根据有一个角是直角的平行四边形是矩形即可证明..
（1）∵ AB∥CD，
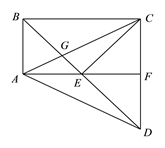
∴ ∠ABE=∠EDC.
∵ ∠BEA=∠DEF，
∴ △ABE∽△FDE.
∴ .
∵ E是BD的中点，
∴ BE=DE.
∴ AB=DF.
∵ F是CD的中点，
∴ CF=FD.
∴ CD=2AB.
∵ ∠ABE=∠EDC，∠AGB=∠CGD，
∴ △ABG∽△CDG.
∴ .
（2）证明：∵ AB∥CF，AB=CF，
∴ 四边形ABCF是平行四边形.
∵ CE=BE，BE=DE，
∴ CE=ED.
∵ CF=FD，
∴ EF垂直平分CD.
∴ ∠CFA=90°.
∴ 四边形
是矩形.
科目：初中数学 来源： 题型：
【题目】如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB＝20，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒．
（1）数轴上点B表示的数是 ，点P表示的数是 ；（用含t的代数式表示）
（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时，P、Q之间的距离恰好等于2；
（3）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，直接写出多少秒时，P、Q之间的距离恰好等于2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法：
①连接两点间的线段叫这两点的距离；
②木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点之间，线段最短；
③若
三点在同一直线上，且
，则
是线段
的中点；
④若
，则有
．
其中一定正确的是_________(把你认为正确结论的序号都填上) ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在图1﹣﹣图4中，菱形ABCD的边长为3，∠A=60°，点M是AD边上一点，且DM=
AD，点N是折线AB﹣BC上的一个动点．
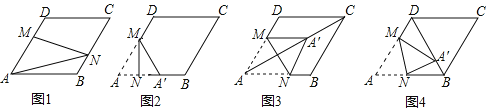
（1）如图1，当N在BC边上，且MN过对角线AC与BD的交点时，则线段AN的长度为 ．
（2）当点N在AB边上时，将△AMN沿MN翻折得到△A′MN，如图2，
①若点A′落在AB边上，则线段AN的长度为 ；
②当点A′落在对角线AC上时，如图3，求证：四边形AM A′N是菱形；
③当点A′落在对角线BD上时，如图4，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
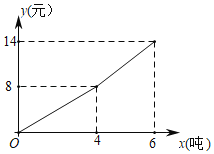
【题目】我国很多城市水资源缺乏，为了加强居民的节水意识，某市制定了每月用水4吨以内（包括4吨）和用水4吨以上收费标准（收费标准：每吨水的价格）某用户每月应交水费y（元）与用水量x（吨）之间关系的图象如图：
（1）说出自来水公司在这两个用水范围内的收费标准；
（2）当x＞4时，求因变量y与自变量x之间的关系式；
（3）若某用户该月交水费26元，求他用了多少吨水？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等腰直角三角形ABC中，
，
，D是AB的中点，E、F分别是AC、BC上的点（点E不与端点A、C重合），连接EF并取EF的中点O，连接DO并延长至点G，使
，连接DE、GE、GF.
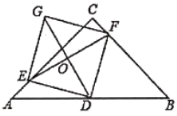
（1）求证：四边形EDFG是平行四边形；
（2）若
，探究四边形EDFG的形状？
（3）在（2）的条件下，当E点在何处时，四边形EDFG的面积最小，并求出最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明对某市出租汽车的计费问题进行研究，他搜集了一些资料，部分信息如下：
收费项目 | 收费标准 |
3公里以内收费 | 13元 |
基本单价 | 2.3元/公里 |
…… | …… |
备注：出租车计价段里程精确到500米；出租汽车收费结算以元为单位，元以下四舍五入。
小明首先简化模型，从简单情形开始研究：①只考虑白天正常行驶（无低速和等候）；②行驶路程3公里以上时，计价器每500米计价1次，且每1公里中前500米计价1.2元，后500米计价1.1元.
下面是小明的探究过程，请补充完整：
记一次运营出租车行驶的里程数为
（单位：公里），相应的实付车费为
（单位：元）.
（1）下表是y随x的变化情况
行驶里程数x | 0 | 0＜x＜3.5 | 3.5≤x＜4 | 4≤x＜4.5 | 4.5≤x＜5 | 5≤x＜5.5 | … |
实付车费y | 0 | 13 | 14 | 15 | … |
（2）在平面直角坐标系
中，画出当
时随变化的函数图象；
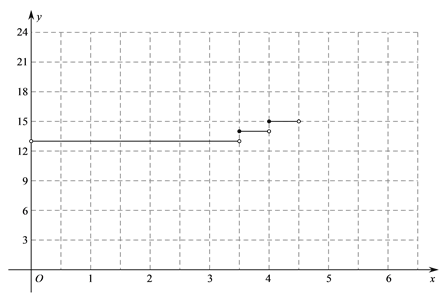
（3）一次运营行驶公里（
）的平均单价记为
（单位：元/公里），其中
.
①当
和
时，平均单价依次为
，则的大小关系是____________；（用“＜”连接）
②若一次运营行驶公里的平均单价不大于行驶任意
（
）公里的平均单价
，则称这次行驶的里程数为幸运里程数.请在上图中轴上表示出
（不包括端点）之间的幸运里程数的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
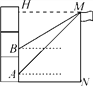
【题目】如图，小明所在教学楼的每层高度为3.5 m，为了测量旗杆MN的高度，他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°，他在二楼窗台B处测得M的仰角为31°，已知每层楼的窗台离该层的地面高度均为1 m.
(1)AB＝________m；
(2)求旗杆MN的高度．(结果保留两位小数)
(参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果. 随着实验次数的增加，“钉尖向上”的频率总在一常数附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是_________
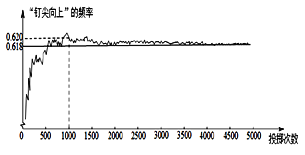
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com