Question

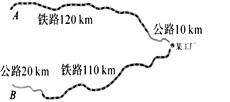
【题目】如图，某工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨2000元的原料运回工厂，制成每吨7500元的产品运到B地．已知公路运价为2元/ (吨·千米)，铁路运价为 1.5元/(吨·千米)，且这两次运输共支出公路运输费2.6万元，铁路运输费15.6万元。

求：(1)该工厂从A地购买了多少吨原料？ 制成运往B地的产品多少吨？

(2)若不计人力成本，这批产品盈利多少元？ （盈利=销售款-原料费-运输费）

Answer 1

【答案】(1) 工厂从A地购买了500吨原料，制成运往B地的产品400吨; (2)不计人力成本，这批产品盈利1818000元．

【解析】试题分析：（1）设工厂从A地购买了x吨原料，制成运往B地的产品y吨，依据公路总运费等于2.6万，铁路总运费等于15.6万列出关于x与y的二元一次方程组，求出方程组的解得到x与y的值即可；

（2）根据盈利＝销售款－原料费－运输费，即可求出所求的结果；

试题解析：

（1）设工厂从A地购买了x吨原料，制成运往B地的产品y吨．

依题意

整理得

解得

答：工厂从A地购买了500吨原料，制成运往B地的产品400吨．

（2）依题意得400×75000－500×2000－26000－156000

＝1818000(元)，

答：不计人力成本，这批产品盈利1818000元．