
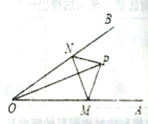
【题目】如图,点![]() 是
是![]() 内任意点,
内任意点,![]() 分别是射线OA,和射线OB上的动点,
分别是射线OA,和射线OB上的动点,![]() 周长的最小值为8cm,则
周长的最小值为8cm,则![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
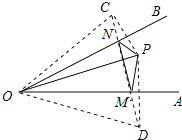
分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,由对称的性质得出PM=DM,OP=OC,∠COA=∠POA;PN=CN,OP=OD,∠DOB=∠POB,得出∠AOB=![]() ∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
解:分别作点P关于OA、OB的对称点C、D,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB=![]() ∠COD,
∠COD,
∵△PMN周长的最小值是8cm,
∴PM+PN+MN=8,
∴DM+CN+MN=8,
即CD=8=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°;
故选:A.


科目:初中数学 来源: 题型:
【题目】关于二次函数![]() ,以下结论:①抛物线交
,以下结论:①抛物线交![]() 轴有两个不同的交点;②不论
轴有两个不同的交点;②不论![]() 取何值,抛物线总是经过一个定点;③设抛物线交
取何值,抛物线总是经过一个定点;③设抛物线交![]() 轴于
轴于![]() 、
、![]() 两点,若
两点,若![]() ,则
,则![]() ;④抛物线的顶点在
;④抛物线的顶点在![]() 图象上;⑤抛物线交
图象上;⑤抛物线交![]() 轴于
轴于![]() 点,若
点,若![]() 是等腰三角形,则
是等腰三角形,则![]() ,
,![]() ,
,![]() .其中正确的序号是( )
.其中正确的序号是( )
A. ①②⑤ B. ②③④ C. ①④⑤ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折.
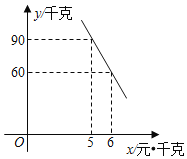
(1)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(2)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O.
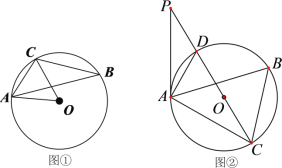
(1)如图①,连接OA,OC,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,直径CD的延长线与过点A的切线相交于点P.若![]() ,⊙O的半径为2,求AD,PD的长.
,⊙O的半径为2,求AD,PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个![]() 奖品和2个
奖品和2个![]() 奖品共需120元;购买5个
奖品共需120元;购买5个![]() 奖品和4个
奖品和4个![]() 奖品共需210元.
奖品共需210元.
(1)求![]() ,
,![]() 两种奖品的单价;
两种奖品的单价;
(2)学校准备在获奖的2名男生3名女生中选两名同学参加县上的比赛,请问选中两名选手都是女孩的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推动阳光体育运动的广泛开展,引导学生走向大自然,走到阳光下积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如图所示两个统计图,请根据相关信息,解答下列问题:
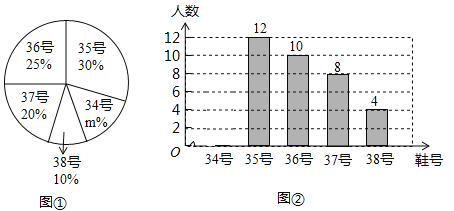
(1)求本次抽样调查的学生人数
(2)通过计算补全条形统计图和扇形统计图;
(3)若学生计划购买200双运动鞋,建议购买35号运动鞋约多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
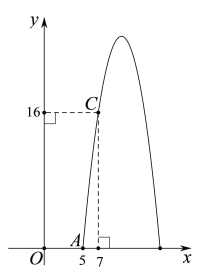
【题目】如图,某商品每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元)之间满足函数
(元)之间满足函数![]() ,其图象与
,其图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在该图象上,点
在该图象上,点![]() ,
,![]() 的坐标见图所示.
的坐标见图所示.
(1)求出这个函数的解析式;
(2)销售价为多少元时,该商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com