
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点G、H在线段DE上,且DG=GH=HE
(1)求证:四边形OGCH是平行四边形;
(2)当点C在弧AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;
(3)求证: 是定值.
是定值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
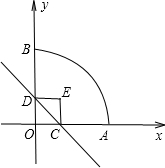 是
是 | AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
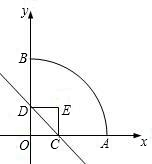 标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:
标系.如图所示、正方形两个顶点C、D分别在x轴、y轴正半轴上移动、设OC=x,OA=3,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
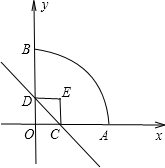 是______;
是______; 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(81):3.4 弧长和扇形的面积,圆锥的侧面展开图(解析版) 题型:解答题
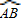 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.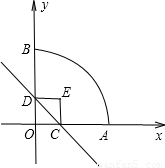
查看答案和解析>>
科目:初中数学 来源:2006年福建省福州市中考数学试卷(大纲卷)(解析版) 题型:解答题
 上时,求正方形与扇形不重合的面积.
上时,求正方形与扇形不重合的面积.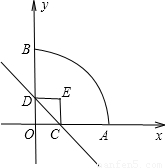
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com