
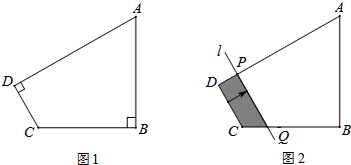
分析 (1)分别延长AD、BC相交于E,在Rt△ABE中,由tanA=$\frac{4}{3}$,AB=3,BC=2,得到BE=4,EC=2,AE=5,通过等角的余角相等得到∠A=∠ECD,由tanA=$\frac{4}{3}$,得cosA=$\frac{3}{5}$,于是得到cos∠ECD=$\frac{CD}{EC}$=$\frac{3}{5}$,即问题可得;
(2)由(1)可知tan∠ECD=$\frac{ED}{CD}=\frac{4}{3}$,得到ED=$\frac{8}{5}$,如图4,由PQ∥DC,可知△EDC~△EPQ,得到比例式$\frac{ED}{EP}=\frac{DC}{PQ}$,求得PQ=$\frac{6}{5}+\frac{3}{4}x$,由S四边形PQCD=S△EPQ-S△EDC,于是得到y=$\frac{1}{2}$PQ•EP-$\frac{1}{2}$DC•ED=$\frac{1}{2}×(\frac{6}{5}+\frac{3}{4}x)×(\frac{8}{5}+x)$-$\frac{1}{2}×\frac{6}{5}×\frac{8}{5}$=${\frac{3}{8}x}^{2}+\frac{6}{5}x$,于是当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,得到DM=ED=$\frac{8}{5}$,于是结论可得.
解答 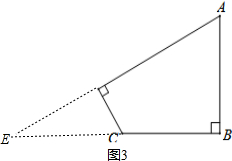 解:(1)如图(3),分别延长AD、BC相交于E,
解:(1)如图(3),分别延长AD、BC相交于E,
在Rt△ABE中,
∵tanA=$\frac{4}{3}$,AB=3,BC=2,
∴BE=4,EC=2,AE=5,
又∵∠E+∠A=90°,∠E+∠ECD=90°,
∴∠A=∠ECD,
由tanA=$\frac{4}{3}$,得cosA=$\frac{3}{5}$,
∴cos∠ECD=$\frac{CD}{EC}$=$\frac{3}{5}$,
∴CD=$\frac{6}{5}$;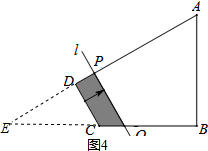
(2)如图4,由(1)可知tan∠ECD=$\frac{ED}{CD}=\frac{4}{3}$,
∴ED=$\frac{8}{5}$,
如图4,由PQ∥DC,可知△EDC~△EPQ,
∴$\frac{ED}{EP}=\frac{DC}{PQ}$,
∴$\frac{\frac{8}{5}}{\frac{8}{5}+x}=\frac{\frac{6}{5}}{PQ}$,即PQ=$\frac{6}{5}+\frac{3}{4}x$,
∵S四边形PQCD=S△EPQ-S△EDC,
∴y=$\frac{1}{2}$PQ•EP-$\frac{1}{2}$DC•ED=$\frac{1}{2}×(\frac{6}{5}+\frac{3}{4}x)×(\frac{8}{5}+x)$-$\frac{1}{2}×\frac{6}{5}×\frac{8}{5}$=${\frac{3}{8}x}^{2}+\frac{6}{5}x$,
∴当Q点到达B点时,点P在M点处,
由EC=BC,DC∥PQ,
∴DM=ED=$\frac{8}{5}$,
∴自变量x的取值方范围为:0<x≤$\frac{8}{5}$.
点评 本题考查了相似三角形的判定和性质,平移的性质,求函数的解析式,解直角三角形,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
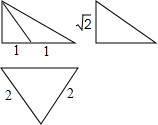 一个棱锥的三视图如图所示,则其左视图直角三角形的面积是( )
一个棱锥的三视图如图所示,则其左视图直角三角形的面积是( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
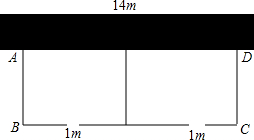 如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由.
如图,要建一个长方形养鸡场(分为两片),养鸡场的一边靠着一面长14m的墙,另几条边及中间隔开的边用总长22m的竹篱围成,每片养鸡场的前面各开一扇宽为1m的门,门用其他材料另外制作,如果要围成总面积为45m2的养鸡场,设这个养鸡场的宽AB=x米,则A、D两点的距离可用含x的分式表示为$\frac{45}{24-3x}$,根据竹篱总长为22m,可列分式方程$\frac{45}{24-3x}$+3x-2=22,x=5满足你所列的方程并符合题意吗?x=3呢?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
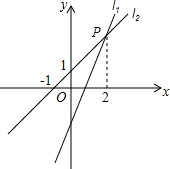 过点(0,-2)的直线l1:y1=kx+b(k≠0)与直线l2:y2=x+1交于点P(2,m).
过点(0,-2)的直线l1:y1=kx+b(k≠0)与直线l2:y2=x+1交于点P(2,m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com