
(10分)如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.
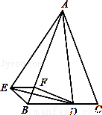
(1)求证:BE=CD;
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明.
(1)见解析 (2)菱形
【解析】
试题分析:(1)根据条件证明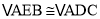 可得;(2)画出较标准的图形,可猜想是菱形,通过证明△ABD≌△ABE,结合其他条件证明BD=BE=EF=FD即可.
可得;(2)画出较标准的图形,可猜想是菱形,通过证明△ABD≌△ABE,结合其他条件证明BD=BE=EF=FD即可.
试题解析:证明:(1)∵△ABC是等腰三角形,顶角∠BAC=α(α<60°),线段AD绕点A顺时针旋转α到AE,
∴AB=AC,
∴∠BAE=∠CAD,
在△ACD和△ABE中,
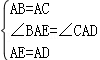 ,
,
∴△ACD≌△ABE(SAS),
∴BE=CD;
(2)∵AD⊥BC,
∴BD=CD,
∴BE=BD=CD,∠BAD=∠CAD,
∴∠BAE=∠BAD,
在△ABD和△ABE中,
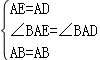 ,
,
∴△ABD≌△ABE(SAS),
∴∠EBF=∠DBF,
∵EF∥BC,
∴∠DBF=∠EFB,
∴∠EBF=∠EFB,
∴EB=EF,
∴BD=BE=EF=FD,
∴四边形BDFE为菱形.
考点:1.图形的旋转;2.全等三角形的判定与性质;3. 菱形的判定.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.

科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片九年级下学期第一次月考数学试卷(解析版) 题型:选择题
已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为 ( )
A.3 B.-1 C.4 D.4或-1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省联盟九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(14分)如图,在平面直角坐标系中,抛物线y=﹣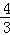 x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
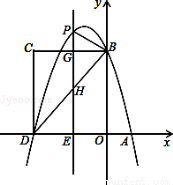
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省联盟九年级下学期第一次月考数学试卷(解析版) 题型:填空题
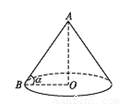
某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO=8米,母线AB与底面半径OB的夹角为α,tan α=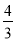 ,则此圆锥的侧面积是__________平方米(结果保留π).
,则此圆锥的侧面积是__________平方米(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省联盟九年级下学期第一次月考数学试卷(解析版) 题型:填空题
有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是
查看答案和解析>>
科目:初中数学 来源: 题型:
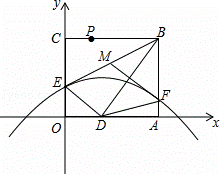
如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5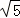 ,且
,且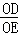 =
=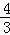 ,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=﹣
,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=﹣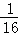 x2+
x2+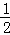 x+c经过点E,且与AB边相交于点F.
x+c经过点E,且与AB边相交于点F.
(1)求证:△ABD∽△ODE;
(2)若M是BE的中点,连接MF,求证:MF⊥BD;
(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com