
反比例函数y= (k为常数,k≠0)的图象是双曲线.当k>0时,双曲线两个分支分别在
(k为常数,k≠0)的图象是双曲线.当k>0时,双曲线两个分支分别在
一、三象限,在每一个象限内,y随x的增大而减小(简称增减性);反比例函数的图象关于
原点对称(简称对称性).
 这些我们熟悉的性质,可以通过说理得到吗?
这些我们熟悉的性质,可以通过说理得到吗?
【尝试说理】
我们首先对反比例函数y= (k>0)的增减性来进行说理.
(k>0)的增减性来进行说理.
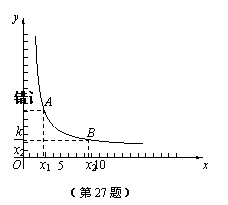
如图,当x>0时.
在函数图象上任意取两点A、B,设A(x1, ),B(x2,
),B(x2, ),
),
且0<x1< x2.
下面只需要比较 和
和 的大小.
的大小.
 —
— =
=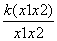 .
.
∵0<x1< x2,∴x1-x2<0,x1 x2>0,且 k>0.
∴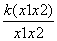 <0.即
<0.即 <
< .
.
这说明:x1< x2时, >
> .也就是:自变量值增大了,对应的函数值反而变小了.
.也就是:自变量值增大了,对应的函数值反而变小了.
即:当x>0时,y随x的增大而减小.
同理,当x<0时,y随x的增大而减小.
(1)试说明:反比例函数y=  (k>0)的图象关于原点对称.
(k>0)的图象关于原点对称.
【运用推广】
 (2)分别写出二次函数y=ax2 (a>0,a为常数)的对称性和增减性,并进行说理.
(2)分别写出二次函数y=ax2 (a>0,a为常数)的对称性和增减性,并进行说理.
对称性: ;
增减性: .
说理:
(3)对于二次函数y=ax2+bx+c (a>0,a,b,c为常数),请你从增减性的角度,简要解释为何当x=—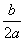 时函数取得最小值.
时函数取得最小值.
(1)在反比例函数y= (k>0)的图象上任取一点P(m,n),于是:mn=k.
(k>0)的图象上任取一点P(m,n),于是:mn=k.
那么点P关于原点的对称点为P1 (-m,-n).而(-m)(-n)=mn=k,
(-m,-n).而(-m)(-n)=mn=k,
这说明点P1也必在这个反比例函数y= 的图象上.
的图象上.
所以反比例函数y=  (k>0)的图象关于原点对称.
(k>0)的图象关于原点对称.
(2)对称性:二次函数y=ax2 (a>0,a为常数)的图象关于y轴成轴对称.
增减性:当x>0时,y随x增大而增大;当x<0时,y随x增大而减小.
理由如下:
①在二次函数y=ax2 (a>0,a为常数) 的图象上任取一点Q(m,n),于是n=am2.
那么点Q关于y轴的对称点Q1(-m,n).而n=a(-m)2,即n=am2.
这说明点Q1也必在在二次函数y=ax2 (a>0,a为常数) 的图象上.
∴二次函数y=ax2 (a>0,a为常数)的图象关于y轴成轴对称,
②在二次函数y=ax2 (a>0,a为常数)的图象上任取两点A、B,设A(m,am2),
B(n,an2) ,且0<m<n.
则an2-am2=a(n+m)(n-m)
∵n>m>0,
∴n+m>0,n-m>0;
∵a>0,
∴an2-am2=a(n+m)(n-m)>0.即an2>am2.
而当m<n<0时,
n+m<0,n-m>0;
∵a>0,
∴an2-am2=a(n+m)(n-m)<0.即an2<am2.
这说明,当x>0时,y随x增大而增大;当x<0时,y随x增大而减小.
(3)二次函数y=ax2+bx+c (a>0,a,b,c为常数) 的图象可以由y=ax2的图象通过平
移得到,关于直线x=—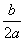 对称,当x=—
对称,当x=—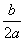 时,y=
时,y=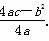 .
.
由(2),当x≥—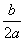 时,y随x增大而增大;也就是说,只要自变量x≥—
时,y随x增大而增大;也就是说,只要自变量x≥—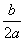 ,其对应
,其对应
的函数值y≥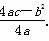 ;而当x≤—
;而当x≤—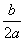 时,y随x增大而减小,也就是说,只要自变量x
时,y随x增大而减小,也就是说,只要自变量x
≤—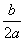 ,其对应的函数值y≥
,其对应的函数值y≥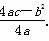 .
.
综上,对于二次函数y=ax2+bx+c (a>0,a,b,c为常数),当x=—
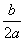 时取得最小值
时取得最小值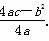


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
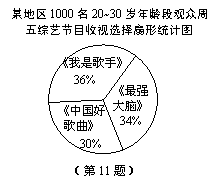
调查机构对某地区1 000名20~30岁年龄段观众周五综艺节目的收视选择进行了调查,相关统计图如下,请根据图中信息,估计该地区 20 000名20~30岁年龄段观众选择观看《最强大脑》的人数约为 人.
20 000名20~30岁年龄段观众选择观看《最强大脑》的人数约为 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
某批发商以40元/千克的成本价购入了某产品700千克,据市场预测,该产品的
销售价y(元/千克)与保存时间x(天)的函数关系为y=50+2x,但保存这批产品平均每天
将损耗15千克,且最多保存15天.另外,批发商每天保存该批产品的费用为50元.
(1)若批发商在保存该产品5天时一次性卖出,则可获利 元.
(2)如果批发商希望通过这批产品卖出获利10000元,则批发商应在保存该产品多少
天时一次性卖出?
查看答案和解析>>
科目:初中数学 来源: 题型:
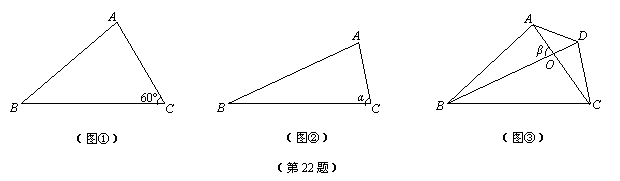
(1)如图①,若BC=6,AC=4,∠C=60°,求△ABC的面积S△ABC ;
(2)如图②,若BC=a,AC=b,∠C=α,求△ABC的面积S△ABC ;
(3)如图③,四边形ABCD,若AC=m,BD=n,对角线AC、BD交于O点,它们所成
的锐角为β.求四边形ABCD的面积S四边形ABCD .
查看答案和解析>>
科目:初中数学 来源: 题型:
某停车场的收费 标准如下:中型汽车的停车费为
标准如下:中型汽车的停车费为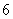 元/辆,小型汽车的停车费为
元/辆,小型汽车的停车费为
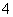 元/辆.现在停车场共有
元/辆.现在停车场共有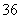 辆中、小型汽车,这些车共缴纳停车费
辆中、小型汽车,这些车共缴纳停车费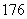 元.问中、小
元.问中、小
型汽车各有多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com