
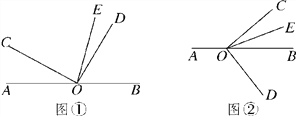
【题目】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=![]() ,直接写出∠DOE的度数(用含
,直接写出∠DOE的度数(用含![]() 的代数式表示);
的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
【答案】见解析
【解析】试题分析:(1)由已知可求出∠BOC=180°-∠AOC=150°,再由∠COD是直角,OE平分∠BOC求出∠DOE的度数;
(2)由(1)可得出结论∠DOE=![]() ∠AOC,从而用含a的代数式表示出∠DOE的度数;
∠AOC,从而用含a的代数式表示出∠DOE的度数;
(3)①由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE,则得∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),从而得出∠AOC和∠DOE的度数之间的关系.
试题解析:(1)由已知得∠BOC=180°-∠AOC=150°,
又∠COD是直角,OE平分∠BOC,
∴∠DOE=∠COD-![]() ∠BOC=90°-
∠BOC=90°-![]() ×150°=15°.
×150°=15°.
(2)∠DOE=![]()
![]() .
.
由(1)知∠DOE=∠COD-![]() ∠BOC=90°,
∠BOC=90°,
∴∠DOE=90°-![]() (180°-∠AOC)=
(180°-∠AOC)= ![]() ∠AOC=
∠AOC=![]()
![]() .
.
(3)∠AOC=2∠DOE. 理由如下:
∵∠COD是直角,OE平分∠BOC,∴∠COE=∠BOE=90°-∠DOE,
∴∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),
∴∠AOC=2∠DOE.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF. 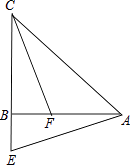
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列推证过程补充完整. 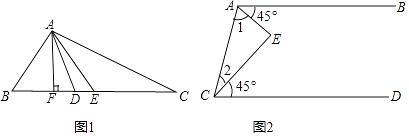
(1)如图1,在△ABC中,AE是中线,AD是角平分线,AF是高.
①BE== ![]() ;
;
②∠BAD== ![]() ;
;
③∠AFB==90°;
④S△ABC= .
(2)如图2,AB∥CD,∠BAE=∠DCE=45°,
∵AB∥CD
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= .
查看答案和解析>>
科目:初中数学 来源: 题型:
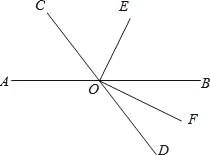
【题目】如图,直线AB与CD相交于O.OF是∠BOD的平分线,OE⊥OF.
(1)若∠BOE比∠DOF大38°,求∠DOF和∠AOC的度数;
(2)试问∠COE与∠BOE之间有怎样的大小关系?请说明理由.
(3)∠BOE的余角是 ,∠BOE的补角是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①三点确定一个圆;②任何三角形有且只有一个内切圆;③相等的圆心角所对的弧相等;④正多边形一定是中心对称图形,其中真命题有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A和B两点在线段EF的中垂线上,且∠EBF=100°,∠EAF=70°,则∠AEB等于( )
A.95°
B.15°
C.95°或15°
D.170°或30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com