
| AM |
| AD |

| BE |
| AE |
| 5 |
| 3 |
| 5 |
| 3 |
| 1 |
| 2 |
| BE-CF |
| AM |
| EK |
| AM |
| KF |
| AB |
| BE-BK |
| AM |
| BC |
| AB |
| BE-CF |
| AM |
| 1 |
| 2 |
|
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
| BE |
| AE |
| ||
|
| 5 |
| 3 |
|
|
| BE-CF |
| AM |
| 1 |
| 2 |
| EK |
| AM |
| KF |
| AB |
| BE-BK |
| AM |
| BC |
| AB |
| BE-CF |
| AM |
| 1 |
| 2 |
| BE-CF |
| AM |


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
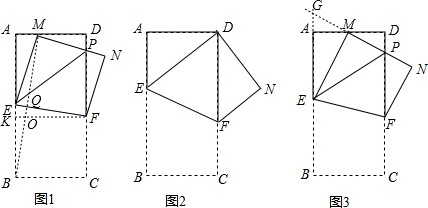
名师指导一卷通系列答案科目:初中数学 来源:2013年湖北省武汉市中考数学模拟试卷(十六)(解析版) 题型:解答题
 =n,其中0<n≤1.
=n,其中0<n≤1.
 =______;
=______; (M为AD的中点),m的值发生变化时,求证:EP=AE+DP;
(M为AD的中点),m的值发生变化时,求证:EP=AE+DP; 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com