如图.反比例函数y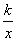＝的图像与一次函数y＝x的图像交于点A.B.点B的横坐标是4．点P是第一象限内反比例函数图像上的动点.且在直线AB的上方． ⑴若点P的坐标是(1.4).直接写出k的值和△PAB的面积, ⑵设直线PA.PB与x轴分别交于点M.N.求证:△PMN是等腰三角形, ⑶设点Q是反比例函数图像上位于P.B之间的动点(与点P.B不重合).连接AQ. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，反比例函数y＝的图像与一次函数y＝x的图像交于点A、B，点B的横坐标是4．点P是第一象限内反比例函数图像上的动点，且在直线AB的上方．

⑴若点P的坐标是（1，4），直接写出k的值和△PAB的面积；

⑵设直线PA、PB与x轴分别交于点M、N，求证：△PMN是等腰三角形；

⑶设点Q是反比例函数图像上位于P、B之间的动点（与点P、B不重合），连接AQ、BQ，比较∠PAQ与∠PBQ的大小，并说明理由．

练习册系列答案

天利38套对接高考单元专题训练系列答案

最新3年中考利剑中考试卷汇编系列答案

考进名校系列答案

北京市重点城区3年真题2年模拟试卷系列答案

河南省重点中学模拟试卷精选及详解系列答案

成都中考真题精选系列答案

名校密卷四川名校招生真卷60套系列答案

毕业升学真题详解四川十大名校系列答案

王后雄黄冈密卷中考总复习系列答案

赢在微点系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

新世纪百货大楼“宝乐”牌童装平均每天可售出20件，每件盈利40元．为了迎接“六一”儿童节，商场决定采取适当的降价措施．经调査，如果每件童装降价1元，那么平均每天就可多售出2件．要想平均每天销售这种童装盈利1200元，则每件童装应降价多少元？设每件童裝应降价x元，可列方程为　

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在Rt△ABC中，∠ACB＝90⁰，AC=6，BC=8。动点M从点A出发，以每秒1个单位长度的速度沿AB向点B匀速运动；同时，动点N从点B出发，以每秒3个单位长度的速度沿BA向点A匀速运动。过线段MN的中点G作边AB的垂线，垂足为点G，交△ABC的另一边于点P，连接PM、PN，当点N运动到点A时，M、N两点同时停止运动，设运动时间为t秒。

（1）当t＝秒时，动点M、N相遇；

（2）设△PMN的面积为S，求S与t之间的函数关系式；

（3）取线段PM的中点K，连接KA、KC，在整个运动过程中，△KAC的面积是否变化？若变化，直接写出它的最大值和最小值；若不变化，请说明理由。

查看答案和解析>>

科目：初中数学 来源： 题型：

数学家歌德巴赫通过研究下面一系列等式，作出了一个著名的猜想．

4＝2＋2；　　　　　 12＝5＋7；

6＝3＋3；　　　　　 14＝3＋11＝7＋7；

8＝3＋5；　　　　　16＝3＋13＝5＋11；

10＝3＋7＝5＋5　　　18＝5＋13＝7＋11；

…

通过这组等式，你发现的规律是_______________________________________（请用文字语言表达）．

查看答案和解析>>

科目：初中数学 来源： 题型：

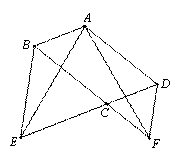
如图，在□ABCD中，∠BCD＝120°，分别延长DC、BC到点E，F，使得△BCE和△CDF都是正三角形．

⑴求证：AE＝AF；

⑵求∠EAF的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：

下列四个命题中，真命题是（　　）

	A．	“任意四边形内角和为360°”是不可能事件
	B．	“湘潭市明天会下雨”是必然事件
	C．	“预计本题的正确率是95%”表示100位考生中一定有95人做对
	D．	抛掷一枚质地均匀的硬币，正面朝上的概率是