
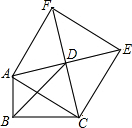
 如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.
如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.分析 (1)由菱形的性质得出∠ABC+∠ADC=180°,证出A、B、C、D四点共圆,由圆周角定理得出∠DAC=∠CBD=45°,∠CAF=2∠DAC=90°,即可得出结论;
(2)作DM⊥AB于M,DN⊥BC于N,得出DM=DN=$\frac{\sqrt{2}}{2}$BD=4,由三角形和四边形的面积得出S四边形ABCD=S△ABC+S△ADC=S△ABD+S△BCD,得出$\frac{3}{2}$BC+$\frac{1}{4}$(BC2+9)=6+2BC,解方程即可.
解答 (1)解:四边形ACEF是正方形;理由如下:
∵BD平分∠ABC,∠ABC=90°,
∴∠CBD=∠ABD=$\frac{1}{2}$∠ABC=45°,AC2=BC2+AB2=BC2+9,
∵四边形ACEF是菱形,
∴AE⊥CF,∠DAC=∠DAF=$\frac{1}{2}$∠CAF,
∴∠ADC=90°,
∴∠ABC+∠ADC=180°,
∴A、B、C、D四点共圆,
∴∠DAC=∠CBD=45°,
∴∠CAF=2∠DAC=90°,
∴四边形ACEF是正方形;
(2)解:作DM⊥AB于M,DN⊥BC于N,如图所示:
则△BDM和△BDN是等腰直角三角形,
∴DM=DN=$\frac{\sqrt{2}}{2}$BD=4,
∴S△ABD=$\frac{1}{2}$AB×DM=$\frac{1}{2}$×3×4=6,
∵S△ABC=$\frac{1}{2}$AB×BC=$\frac{3}{2}$BC,
S△BDC=$\frac{1}{2}$BC×DN=2BC,S△ACD=$\frac{1}{4}$S正方形ACEF=$\frac{1}{4}$AC2=$\frac{1}{4}$(BC2+9),
S四边形ABCD=S△ABC+S△ADC=S△ABD+S△BCD
∴$\frac{3}{2}$BC+$\frac{1}{4}$(BC2+9)=6+2BC
解得:BC=5或BC=-3(舍去),
∴BC=5.
点评 本题考查了正方形的判定与性质、菱形的性质、四点共圆、圆周角定理、角平分线的性质、等腰直角三角形的性质、三角形面积的计算方法等知识;本题综合性强,难度较大,特别是(2)中,需要作辅助线通过四边形和三角形的面积关系得出方程才能得出结果.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是( )
如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是( )| A. | △ADC≌△BDH | B. | HE=EC | C. | AH=BD | D. | △AHE≌△BHD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
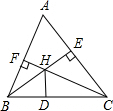 如图,在△ABC中,∠ABC=60°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,HD是∠BHC的平分线,求∠ABE,∠ACF和∠CHD的度数.
如图,在△ABC中,∠ABC=60°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,HD是∠BHC的平分线,求∠ABE,∠ACF和∠CHD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
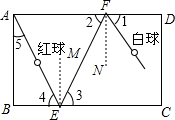 如图,选择适当的方向击打白球,可使白球经过两次反弹后将红球撞入底袋,白球在运动过程中,∠1=∠2,∠3=∠4,如果红球与洞口的连线与台球桌边缘的夹角∠5=25°,那么选择∠1是多少度,才能保证红球能直接入袋?为什么?
如图,选择适当的方向击打白球,可使白球经过两次反弹后将红球撞入底袋,白球在运动过程中,∠1=∠2,∠3=∠4,如果红球与洞口的连线与台球桌边缘的夹角∠5=25°,那么选择∠1是多少度,才能保证红球能直接入袋?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com