
分析 先将原式化为完全平方的形式,再开方化简即可解答本题.
解答 解:$\sqrt{y+2+3\sqrt{2y-5}}$-$\sqrt{y-2+\sqrt{2y-5}}$
=$\sqrt{(\sqrt{y-\frac{5}{2}})^{2}+2×\frac{3\sqrt{2}\sqrt{y-\frac{5}{2}}}{2}+(\frac{3\sqrt{2}}{2})^{2}}-$$\sqrt{(\sqrt{y-\frac{5}{2}})^{2}+2×\frac{\sqrt{2}\sqrt{y-\frac{5}{2}}}{2}+(\frac{\sqrt{2}}{2})^{2}}$
=$\sqrt{(\sqrt{y-\frac{5}{2}}+\frac{3\sqrt{2}}{2})^{2}}-\sqrt{(\sqrt{y-\frac{5}{2}}+\frac{\sqrt{2}}{2})^{2}}$
=$\sqrt{y-\frac{5}{2}}+\frac{3\sqrt{2}}{2}-(\sqrt{y-\frac{5}{2}}+\frac{\sqrt{2}}{2})$
=$\sqrt{y-\frac{5}{2}}+\frac{3\sqrt{2}}{2}-\sqrt{y-\frac{5}{2}}-\frac{\sqrt{2}}{2}$
=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查二次根式的化简求值,解题的关键是能观察出原式能先将根号内的式子化为完全平方的形式.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 3 | C. | -3 | D. | -4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
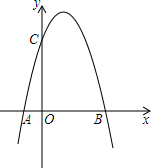 如图,在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA;
如图,在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA;查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳老河口九年级3月月考数学试卷(解析版) 题型:判断题
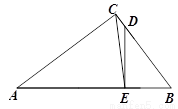
如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点D在边BC上,BD=5CD,DE⊥AB,垂足为E.
(1)求BE的长;
(2)求∠BCE的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com