
如图,在平面直角坐标系中,将一块腰长为![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的啦标为(-1,0),点B在抛物线![]() 上,
上,
1.点A的坐标为__________,点B的坐标为___________;抛物线的解析式为_________;
2.在抛物线上是否还存在点P(点B除外),使△ACP是以AC为直角边向直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由
3.若点D是(1)中所求抛物线在第三象限内的一个动点,连结BD、CD。当△BCD的面积最大时,求点D的坐标。
4.若点P是(1)中所求抛物线上一个动点,以线段AB、BP为邻边作平形四边形ABPQ。当点Q落在x轴上时,直接写出点P的坐标.
1.A(0,2),B(-3,1).![]()
2.存在点P(点B除外),使三角形ACP是以AC为直角边的直角三角形 4分
理由如下:
分情况讨论:
①延长BC交抛物线于点P,连结AP1
因为∠ACB=90°,∴∠ACP=90°
设直线BC的解析式为y=kx+b
将B(-3,1),C(-1,0)代入上式得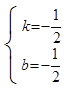
所以![]() 5分
5分
联立方程组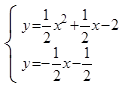 解得
解得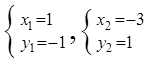 (不符合题意舍去)
(不符合题意舍去)
所以:P1(1,-1) 6分
②过点A作AP2//BC,交抛物线于点P2,P3
设直线AP2的解析式为![]() ,将
,将![]() 代入得
代入得![]()
所以:![]()
联立方程组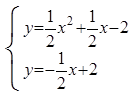 解得:
解得: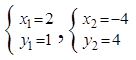
所以:P2(2,1),P3(-4,4)
综上所述:存在点P1(1,-1),P2(2,1),P3(-4,4)(点B除外),使三角形ACP
是以AC为直角边的直角三角形 7分
3.设点D的坐标为(m,![]() ),过点D作DM⊥x轴交直线BC于点M
),过点D作DM⊥x轴交直线BC于点M
所以点M的坐标为(m,![]() ),MD=
),MD=![]() 8分
8分
再设三角形BCD的面积为S。
S=![]() =
=![]() 9分
9分
因为S是m的二次函数,且抛物线开口向下,函数有最大值
即当m=-1时S有最大值2
此时点D的坐标为(-1,-2)
4.(1,-1)。(-2,-1)
解析:(1)根据勾股定理求点A的坐标,点B的坐标,根据点B的坐标求抛物线的解析式
(2)根据延长BC交抛物线于点P,连结AP1,或者过点A作AP2//BC,交抛物线于点
P2,P3构成的三角形进行解答
(3)设点D的坐标为(m,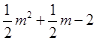 ),过点D作DM⊥x轴交直线BC于点M,求得MD=
),过点D作DM⊥x轴交直线BC于点M,求得MD=![]() ,三角形BCD的面积为
,三角形BCD的面积为![]() ,再根据二次函数的性质求出点D的坐标
,再根据二次函数的性质求出点D的坐标
(4)根据平形四边形的性质求出点P的坐标


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.| BD |
| AB |
| 5 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是| 5 |
| 29 |
| 5 |
| 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com