
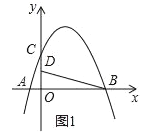
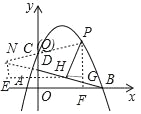
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于点A(﹣2,0)和B(B在A右侧),交y轴于点C,直线y=![]() 经过点B,交y轴于点D,且D为OC中点.
经过点B,交y轴于点D,且D为OC中点.
(1)求抛物线的解析式;
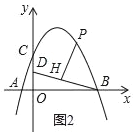
(2)若P是第一象限抛物线上的一点,过P点作PH⊥BD于H,设P点的横坐标是t,线段PH的长度是d,求d与t的函数关系式;
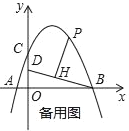
(3)在(2)的条件下,当d=![]() 时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)P(
x+4;(2)P(![]() ,
,![]() );(3)Q(0,4).
);(3)Q(0,4).
【解析】试题分析:(1)首先求出点B坐标,利用待定系数法即可解决问题.
(2)设P(t,﹣![]() t2+
t2+![]() t+4),,由cos∠HPM=cos∠DBO,可得
t+4),,由cos∠HPM=cos∠DBO,可得![]() ,由此构建二次函数,利用二次函数的性质解决问题.
,由此构建二次函数,利用二次函数的性质解决问题.
(3) 过点P作PF⊥x轴于点F,过点H作HG⊥PF于点G,BD与PQ交于点N,过N作NE⊥HG于E.由全等三角形△PHG≌△HNE,的性质,(2)中函数解析式求得点P、N的坐标,然后由直线与抛物线的解析式求得交点Q的坐标.
解:(1)∵y=2kx﹣12k 经过B点,
∴当y=0,x=6,
∴B(6,0),又∵A(﹣2,0),
∴![]() ,
,
解得![]() ,
,
∴y=﹣![]() x2+
x2+![]() x+4.
x+4.
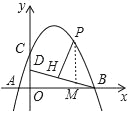
(2)如图,过点P作PM∥y轴交BD于点M,设P(t,﹣![]() t2+
t2+![]() t+4),
t+4),
∵CD=OD,
当x=0时y=4,
∴C(0,4)
∴OD=2,
∴D(0,2),
∴BD=2![]() ,
,
设直线BD解析式为y=mx+n,
∴6m+n=0,n=2,
∴yBD=﹣![]() x+2,
x+2,
∴M(t,﹣![]() t+2),
t+2),
∴PM=﹣![]() t2+
t2+![]() t+2,
t+2,
∵∠HPM=∠DBO,
∴cos∠HPM=cos∠DBO,
∴![]() =
=![]() ,
,
∴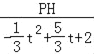 =
=![]() ,
,
∴d=﹣![]() t2+
t2+![]() t+
t+![]() ,
,
∴d=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,PH值最大,
时,PH值最大,
∴P(![]() ,
,![]() ).
).
(3)过点P作PF⊥x轴于点F,过点H作HG⊥PF于点G,BD与PQ交于点N,过N作NE⊥HG于E.
∵∠HPN=45°,PH⊥BD,
∴PH=HN,
∴△PHG≌△HNE,
∴HG=NE,PG=EH,
∵由(2)知,d=﹣![]() t2+
t2+![]() t+
t+![]() ,即:d=﹣
,即:d=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,PH=
时,PH=![]() ,
,
∴P(![]() ,
,![]() ).
).
当PH=![]() 时,HG=
时,HG=![]() PG=
PG=![]() ,
,
∴EH=![]() ,EN=
,EN=![]() ,
,
∴N(﹣![]() ,
,![]() ),P(
),P(![]() ,
,![]() ),
),
∴yPN=![]() x+4,
x+4,
由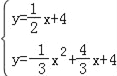 ,
,
解得![]() 或
或![]() ,
,
∴Q(0,4).


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A逆时针旋转80°后得到△A′B′C′(点B的对应点是点B′,点C的对应点是点C′,连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
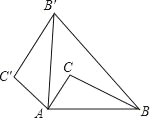
A. 82° B. 80° C. 78° D. 76°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是中线,作
是中线,作![]() 关于
关于![]() 的轴对称图形
的轴对称图形![]() .
.
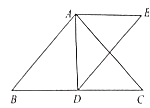
(1)直接写出![]() 和
和![]() 的位置关系;
的位置关系;
(2)连接![]() ,写出
,写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() ,
,![]() 时,在
时,在![]() 上找一点
上找一点![]() ,使得点
,使得点![]() 到点
到点![]() 与到点
与到点![]() 的距离之和最下小,求
的距离之和最下小,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在完成第10章的学习后,遇到了一些问题,请你帮助他.
(1)图1中,当![]() ,试说明
,试说明![]() .
.
(2)图2中,若![]() ,则
,则![]() 吗?请说明理由.
吗?请说明理由.
(3)图3中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ______(直接写出结果,用含x,y,z的式子表示)
______(直接写出结果,用含x,y,z的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
(1)求证:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究规律:我们有可以直接应用的结论:若两条直线平行,那么在一条直线上任取一点,无论这点在直线的什么位置,这点到另一条直线的距离均相等.例如:如图1,两直线![]() ∥
∥![]() ,两点
,两点![]() ,
,![]() 在
在![]() 上,
上,![]() ⊥
⊥![]() 于
于![]() ,
,![]() ⊥
⊥![]() 于
于![]() ,则
,则![]() .
.
如图2,已知直线![]() ∥
∥![]() ,
,![]() ,
,![]() 为直线
为直线![]() 上的两点,
上的两点,![]() .
.![]() 为直线
为直线![]() 上的两点.
上的两点.
(1)请写出图中面积相等的各对三角形: .
(2)如果![]() ,
,![]() ,
,![]() 为三个定点,点
为三个定点,点![]() 在
在![]() 上移动,那么无论
上移动,那么无论![]() 点移动到任何位置,总有: 与
点移动到任何位置,总有: 与![]() 的面积相等;理由是: .
的面积相等;理由是: .

解决问题:
如图3,五边形![]() 是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图4所示的形状,但承包土地与开垦荒地的分界小路(图4中折线
是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图4所示的形状,但承包土地与开垦荒地的分界小路(图4中折线![]() )还保留着,张大爷想过点
)还保留着,张大爷想过点![]() 修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)
修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)
(1)写出设计方案,并在图4中画出相应的图形;
(2)说明方案设计理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
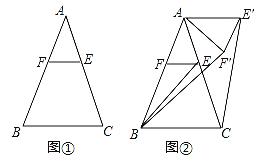
【题目】已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F
(1)如图①,求证:AE=AF;
(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.
①若BF′=6,求CE′的长;
②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com