Question

已知：三角形的三边长为3、4、5，则此三角形的内切圆的半径为________．

Answer 1

1
分析：三角形的三边长为3、4、5，则此三角形的内切圆的半径
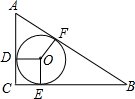
解答：解：如图所示：△ABC中，AC=3，BC=4，AB=5，
∵3²+4²=5²，即AC²+BC²=AB²，
∴△ABC是直角三角形，
设△ABC内切圆的半径为R，切点分别为D、E、F，
∵CD=CE，BE=BF，AF=AD，
∵OD⊥AC，OE⊥BC，
∴四边形ODCE是正方形，即CD=CE=R，
∴AC-CD=AB-BF，即3-R=5-BF①
BC-CE=AB-AF，即4-R=BF②，
①②联立得，R=1．
故答案为：1．
点评：本题考查的是三角形的内切圆与内心，涉及到勾股定理的逆定理、正方形的判定与性质、切线长定理，涉及面较广，难度适中．