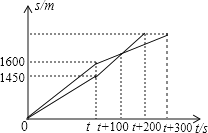
【题目】在一次越野赛跑中，当小明跑了1600m时，小刚跑了1450m，此后两人分别调整速度，并以各自新的速度匀速跑，又过100s时小刚追上小明，200s时小刚到达终点，300s时小明到达终点．他们赛跑使用时间t（s）及所跑距离如图s（m），这次越野赛的赛跑全程为 m？
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目：初中数学 来源： 题型：
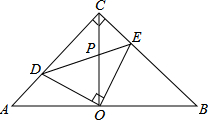
【题目】如图，在等腰直角△ABC中，∠ACB=90°，O是斜边AB的中点，点D，E分别在直角边AC，BC上，且∠DOE=90°，DE交OC于点P．则下列结论：(1)AD+BE=AC；(2)AD2+BE2=DE2；(3)△ABC的面积等于四边形CDOE面积的2倍；(4)OD=OE．其中正确的结论有( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
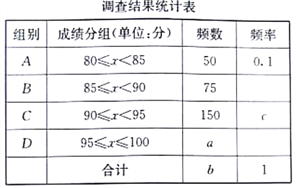
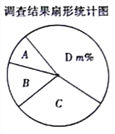
【题目】2018年3月，某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动，活动结束后，随机抽取了部分同学的成绩(x均为整数，总分100分)，绘制了如下尚不完整的统计图表。
根据以上信息解答下列问题
(1)统计表中，a＝ ，b＝ ，c＝ 。
(2)扇形统计图中，m的值为 。“C”所对应的圆心角的度数是 ；
(3)若参加本次竞赛的同学共有5000人，请你估计成绩在95分及以上的学生大约有多少人?
查看答案和解析>>
科目：初中数学 来源： 题型：
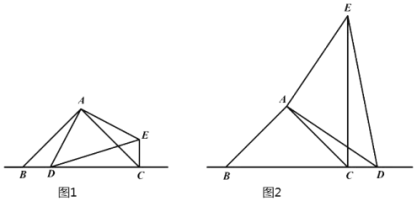
【题目】已知:△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D是等腰直角三角形ABC斜边BC所在直线上一点(不与点B重合).
(1)如图1，当点D在线段BC上时，线段CE、BD之间的位置关系是__________，数量关系是___________；
(2)如图2，当点D在线段BC的延长线上时，探索AD、BD、CD三条线段之间的数量关系，写出结论并证明；
(3)若BD=
CD，直接写出∠BAD的度数。
查看答案和解析>>
科目：初中数学 来源： 题型：
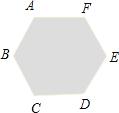
【题目】如图，在正六边形ABCDEF内放入2008个点，若这2008个点连同正六边形的六个顶点无三点共线，则该正六边形被这些点分成互不重合的三角形共_____个.
查看答案和解析>>
科目：初中数学 来源： 题型：
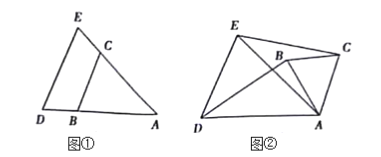
【题目】如图①，在△ABC与△ADE中，AB=AC，AD=AE，∠A是公共角。
（1）BD与CE的数量关系是：BD______CE；
（2）把图①△ABC绕点A旋转一定的角度，得到如图②所示的图形。
①求证：BD＝CE；
②BD与CE所在直线的夹角与∠DAE的数量关系是什么？说明理由。
（3）若AD=10，AB=6，把图①中的△ABC绕点A顺时针旋转α度(0°<α≤360)直接写出BD长度的取值范围。
查看答案和解析>>
科目：初中数学 来源： 题型：
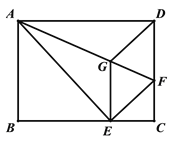
【题目】如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．
（1）求证：四边形EFDG是菱形；
（2）若AG=7、GF=3，求DF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，平面直角坐标系中，矩形OABC的顶点A（6，0）、B（6，4），D是BC的中点．动点P从O点出发，以每秒1个单位的速度，沿着OA、AB、BD运动．设P点运动的时间为t秒（0<t<13）．
（1）写出△POD的面积S与t之间的函数关系式，并求出△POD的面积等于9时点P的坐标；
（2）当点P在OA上运动时，连结CP．问：是否存在某一时刻t，当CP绕点P旋转时，点C能恰好落到AB的中点M处？若存在，请求出t的值并判断此时△CPM的形状；若不存在，请说明理由；
（3）当点P在AB上运动时，试探索当PO+PD的长最短时的直线PD的表达式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
