
分析 (1)$\frac{2000}{x}$=$\frac{2800}{x+10}$表示的等量关系是“该公司购买的玻璃杯与保温杯的数量能相同”; $\frac{2800}{y}$-$\frac{2000}{y}$=10的等量关系是“一个保温杯比一个玻璃杯贵10元”;
(2)假设能相等,设玻璃杯数量是y,得方程$\frac{2800}{y}$-$\frac{2000}{y}$=10,得出答案即可.
解答 解:(1)未知数x表示玻璃杯单价;未知数y玻璃杯数量(或保温杯数量).
(2)$\frac{2800}{y}$-$\frac{2000}{y}$=10
y=80,
经检验y=80是原方程的根,
因此,该公司购买的玻璃杯与保温杯的数量相同.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{500}{x}$+$\frac{45}{x+10}$=24 | B. | $\frac{0.5}{x}$+$\frac{4.5}{x+10}$=$\frac{24}{60}$ | ||
| C. | $\frac{500}{x-10}$+$\frac{4500}{x}$=24 | D. | $\frac{0.5}{x-10}$+$\frac{4.5}{x}$=$\frac{24}{60}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
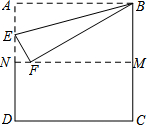 如图,把边长为2的正方形纸片ABCD先对折一次再展开,折痕为MN,然后再沿过点B的线段折叠,使得点A落在MN上的点F处,折痕交AN于点E,则NF的长为( )
如图,把边长为2的正方形纸片ABCD先对折一次再展开,折痕为MN,然后再沿过点B的线段折叠,使得点A落在MN上的点F处,折痕交AN于点E,则NF的长为( )| A. | 2 | B. | 2-$\sqrt{3}$ | C. | $\sqrt{2}$-1 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
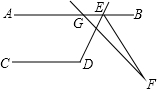 如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )
如图,已知AB∥CD,∠CDE=118°,直线GF与AB交于点G,与∠BED的平分线交于点F,若∠AGF=132°,则∠F的度数为( )| A. | 24° | B. | 12° | C. | 11° | D. | 10° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
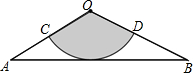 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )| A. | 10 cm | B. | 15 cm | C. | 10$\sqrt{3}$ cm | D. | 20$\sqrt{2}$ cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com