
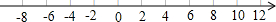 动点A从原点出发向数轴负方向匀速运动,同时,动点B也从原点出发向数轴正方向匀速运动,已知动点A、B运动的速度比是1:4(速度单位:单位长度/秒)3秒后,两动点相距15个单位长度
动点A从原点出发向数轴负方向匀速运动,同时,动点B也从原点出发向数轴正方向匀速运动,已知动点A、B运动的速度比是1:4(速度单位:单位长度/秒)3秒后,两动点相距15个单位长度分析 (1)等量关系为:A的路程+B的路程=15;
(2)原点恰好处在两个动点正中间,说明此时两点到原点的距离相等.等量关系为:A的路程+3=12-B的路程;
(3)C的运动速度为20,时间和A,B运动的时间相等.所以需求出A,B运动的时间.∵是B追A,所以等量关系为:B的路程-A的路程=2×($\frac{9}{5}$+3).
解答 解:(1)设A的速度是x单位长度/秒,则B的速度为4x单位长度/秒,由题意,得
3(x+4x)=15,
解得:x=1,
∴B的速度为4,
∴A、B两点从原点出发运动3秒时,A到达的位置为-3,B到达的位置是12,在数轴上的位置如图:
答:A的速度为1;B的速度为4.
(2)设y秒后,原点恰好处在A、B的正中间.
由题意得:y+3=12-4y,
解得:y=$\frac{9}{5}$.
答:经过$\frac{9}{5}$秒后,原点恰处在A、B的正中间;
(3)设B追上A需时间z秒,则:
4×z-1×z=2×($\frac{9}{5}$+3),
解得:z=$\frac{16}{5}$,
20×$\frac{16}{5}$=64.
答:C点行驶的路程是64长度单位.
点评 本题考查了行程问题的数量关系的运用,相遇问题的数量关系的运用,列一元一次方程解实际问题的运用,数轴的运用,解答时由行程问题的数量关系建立方程是关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com