
| A. | $y=\frac{1}{4}{(x+3)^2}$ | B. | $y=-\frac{1}{4}{(x+3)^2}$ | C. | $y=-\frac{1}{4}{(x-3)^2}$ | D. | $y=\frac{1}{4}{(x-3)^2}$ |
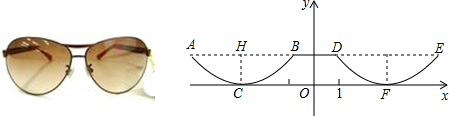
分析 根据题意可以求得点C、点B的坐标,然后根据眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称,从而可以求得点D和点F的坐标,然后设出右轮廓线DFE所在抛物线的函数顶点式,从而可以解答本题.
解答 解:∵眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称,AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,
∴点C的坐标为(-3,0),点B(-1,1),
∴点D(1,1),点F(3,0),
设右轮廓线DFE所在抛物线的函数解析式为:y=a(x-3)2,
则1=a(1-3)2,
解得,a=$\frac{1}{4}$,
∴右轮廓线DFE所在抛物线的函数解析式为:y=$\frac{1}{4}$(x-3)2,
故选D.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,求出抛物线的顶点坐标和经过的点D的坐标,利用二次函数的顶点式解答.


科目:初中数学 来源: 题型:解答题
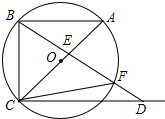 如图.点A、B、C为⊙O上三点,AC为⊙O的直径,AB∥CD,AC=CD.连接BD交AC于点E,交⊙O于点F,AB=$\sqrt{7}$,BC=3.
如图.点A、B、C为⊙O上三点,AC为⊙O的直径,AB∥CD,AC=CD.连接BD交AC于点E,交⊙O于点F,AB=$\sqrt{7}$,BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
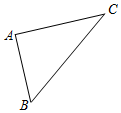 如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )
如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1<k<0 | B. | -4<k<0 | C. | 0<k<1 | D. | 0<k<4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com