
| 单价(元/棵) | 成活率 | 植树费(元/棵) | |
| A | 20 | 90% | 5 |
| B | 30 | 95% | 5 |


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
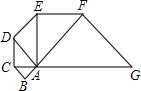 (2013•梅州)如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是
(2013•梅州)如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•梅州)如图,在平面直角坐标系中,A(-2,2),B(-3,-2)
(2013•梅州)如图,在平面直角坐标系中,A(-2,2),B(-3,-2)查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com