

分析 (1)根据数轴上的点表示的数,可得答案;
(2)根据数轴上到一点距离相等的点有两个,分别位于该点的左右,可得答案;
(3)从数轴上找出A点与-3表示的点所连线段的中点,即距A,-3两点的距离都是2的点,然后读出这个数,即可得出B点的对称点;
(4)利用(3)中所求对称中心,以及M、N两点之间的距离为9,即可得出M,N点的位置..
解答 解:(1)由数轴上A、B两点的位置,得A表示1,B表示-2.5.
故答案为:1,-2.5;
(2)观察数轴,与点A的距离为4的点表示的数是-3或5,
故答案为:-3或5;
(3)∵将数轴折叠,A点与-3表示的点重合,
∴两点的对称中心是-1,
∴B点与数0.5重合.
故答案为0.5;
(4)∵两点的对称中心是-1,数轴上M、N两点之间的距离为10(M在N的左侧),
∴M、N两点表示的数分别是:-1-5=-6,-1+5=4.
故答案为-6,4.
点评 此题主要考查了在数轴上解决实际问题的能力,学生要会利用数轴来解决这些问题,找出对称中心是解决问题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:选择题
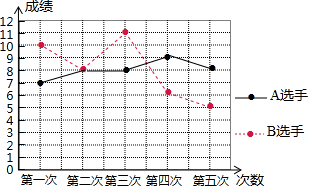 2022年将在北京-张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )
2022年将在北京-张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )| A. | SA2>SB2,应该选取B选手参加比赛 | B. | SA2<SB2,应该选取A选手参加比赛 | ||
| C. | SA2≥SB2,应该选取B选手参加比赛 | D. | SA2≤SB2,应该选取A选手参加比赛 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com