
����Ŀ����ͼ����Rt��ABC�У���B��90����AC��60cm����A��60������D�ӵ�C������CA������4cm/s���ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/s���ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����ts������D��DF��BC�ڵ�F������DE��EF��
��1����֤��AE��DF��
��2���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
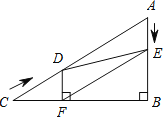
���𰸡���1������������2���ܣ�10����3����t��![]() ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����
ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����
��������
��1������t��ʾ��CD�Լ�AE�ij���Ȼ����ֱ�ǡ�CDF�У�����ֱ�������ε��������DF�ij�������֤����
��2����֤�ı���AEFD��ƽ���ı��Σ���AD��AEʱ���ı���AEFD�����Σ��ݴ˼����з������t��ֵ��
��3���ֱ�ӡ�EDF��90�����DEF��90������������ۼ������.
��1��֤��������Rt��ABC�У���B��90����AC��60cm����A��60����
���C��90������A��30����
��CD��4tcm��AE��2tcm��
�֡���ֱ�ǡ�CDF�У���C��30����
��DF��![]() CD��2tcm��
CD��2tcm��
��DF��AE��
��2���ܣ�
��DF��AB��DF��AE��
���ı���AEFD��ƽ���ı��Σ�
��AD��AEʱ���ı���AEFD�����Σ�
��60��4t��2t��
��ã�t��10��
����t��10ʱ��AEFD�����Σ�
��3���⣺��t��![]() ʱ��DEF��ֱ�������Σ���EDF��90������
ʱ��DEF��ֱ�������Σ���EDF��90������
��t��12ʱ����DEF��ֱ�������Σ���DEF��90������
�������£�
����EDF��90��ʱ��DE��BC��
���ADE����C��30����
��AD��2AE
��CD��4tcm��
��DF��AE��2tcm��
��AD��2AE��4tcm��
��4t+4t��60��
��t��![]() ʱ����EDF��90����
ʱ����EDF��90����
����DEF��90��ʱ��DE��EF��
���ı���AEFD��ƽ���ı��Σ�
��AD��EF��
��DE��AD��
���ADE��ֱ�������Σ���ADE��90����
�ߡ�A��60����
���DEA��30����
��AD��![]() AE��
AE��
AD��AC��CD��60��4t��cm����AE��DF��![]() CD��2tcm��
CD��2tcm��
��AD=tcm��
��60��4t��t��
���t��12��
������������t��![]() ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����.
ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����н�����̣�
���㣺(��5)��![]() ��20.
��20.
�⣺ԭʽ��(��5)��![]() ��20��(��һ��)
��20��(��һ��)
��(��5)��(��1)��(�ڶ���)
����5.������(������)
(1)�����������������������
��һ���ǵ�________���������ԭ����__________________________��
�ڶ����ǵ�________���������ԭ����_______________________��
(2)����ȷ�Ľ������д������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��1����ѧ������ɿ���ѧϰ�����ʽ��������е����ݷ����������ÿ���ʱ������μ�����������ÿλͬѧ������������������Զ�����ܡ�Ǧ����ѡһ�����ѵ����ѵ�������˲��ԣ��ֽ���Ŀѡ�������ѵ��������ʱ����Ͷ�����Գɼ���������������ͳ��ͼ��

������������ṩ����Ϣ�ش��������⣺
��1������ͼ���������ֵ�����Բ�Ľ�Ϊ__________�ȣ��ð��ѧ��__________�ˣ�ѵ��������ʱ����Ͷ��ƽ��ÿ���˵Ľ�������__________��
��2����ʦ������ѡ��Ǧ��ѵ����3��������1��Ů������ѡ����ѧ���Ƚ��в��ԣ������б�������ͼ�ķ�����ǡ��ѡ�����������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ķ���������ij��˾�¹�Ʊ![]() �ɣ�ÿ��
�ɣ�ÿ��![]() Ԫ���±�Ϊ������ÿ�ոùɵ��ǵ���������������չ������У�����λ��Ԫ��
Ԫ���±�Ϊ������ÿ�ոùɵ��ǵ���������������չ������У�����λ��Ԫ��
���� | һ | �� | �� | �� | �� |
ÿ���ǵ� | +1.5 | ��0.7 | ��1.2 | +2 | ��1.8 |
��1������������ʱ��ÿ���Ƕ���Ԫ��
��2��������ÿ����۶���Ԫ����ͼ��Ƕ���Ԫ��
��3����֪��ķ�����Ʊʱ����![]() �������ѣ�����ʱ���踶�ɽ���
�������ѣ�����ʱ���踶�ɽ���![]() �������Ѻ͵�
�������Ѻ͵�![]() ����˰�������ķ������������ǰ��ȫ����Ʊ�������������������Σ�
����˰�������ķ������������ǰ��ȫ����Ʊ�������������������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
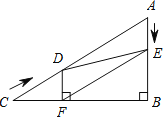
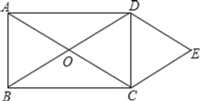
����Ŀ����ͼ��ʾ��O�Ǿ���ABCD�ĶԽ��ߵĽ��㣬��DE//AC��CE//BD��DE��CE�ཻ�ڵ�E��
��֤����1���ı���OCED�����Σ�
��2������OE����AD=5��CD=3��������OCED�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �Ķ���ΪB(1��3)����
�Ķ���ΪB(1��3)����![]() ��Ľ���A�ڵ� (2��0)��(3��0)֮�䣮���½��ۣ�
��Ľ���A�ڵ� (2��0)��(3��0)֮�䣮���½��ۣ�
��![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]() ������
������![]() ����
����![]() ��
��
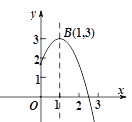
��![]() .������ȷ�Ľ������� ��
.������ȷ�Ľ������� ��
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺̽������y=|x|-1�����ʣ�
С��ͬѧ����ѧϰ�����ľ��飬�Ժ���y=|x|-1��ͼ�������ʽ�����̽����������С����̽�����̣��벹��������
��1���ں���y=|x|-1�У��Ա���x��ȡֵ��Χ��______________��
��2���±���y��x�ļ����Ӧֵ��
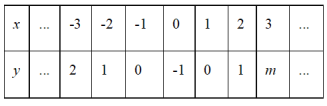
��m=_________��
����A��n��9����B��10��9��Ϊ�ú���ͼ���ϲ�ͬ�����㣬��n=__________��
��3������ͼ����ƽ��ֱ������ϵxOy�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣮����������ĵ㣬�����ú�����ͼ��
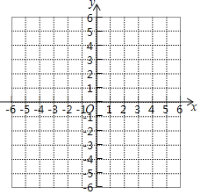
��4����Ϻ���ͼ������⣺
�ٸú�����______(�������ֵ��������Сֵ��)����д�����ֵΪ______��
�ڹ۲캯��y=|x|-1��ͼ��д����ͼ����������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�� 2(2a 2 9b) 3(3a 2 4b)
��2��(![]() a 2 b2)(
a 2 b2)(![]() a b)(
a b)( ![]() a b)
a b)
��3�� (![]() x 2y 3 )2 (3xy)3 (
x 2y 3 )2 (3xy)3 (![]() x 2 y 3)2 ( x)3 2 y 3
x 2 y 3)2 ( x)3 2 y 3
��4���ü�㷽�����㣺9982 9980 16
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com