
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
【答案】(1)EC=EB;(2)ED=EB,理由见解析;(3)ED=EB;拓展应用:C(1,2+![]() ).
).
【解析】
探究结论:(1)只要证明△ACE是等边三角形即可解决问题;
(2)如图2中,结论:ED=EB.想办法证明EP垂直平分线段AB即可解决问题;
(3)结论不变,证明方法类似;
拓展应用:利用(2)中结论,可得CO=CB,设C(1,n),根据OC=CB=AB,构建方程即可解决问题.
探究结论(1),如图1中,
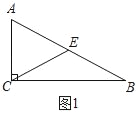
∵∠ACB=90°,∠B=30°,
∴∠A=60°,
∵AC=![]() AB=AE=EB,
AB=AE=EB,
∴△ACE是等边三角形,
∴EC=AE=EB,
故答案为:EC=EB;
(2)如图2中,结论:ED=EB.
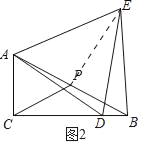
理由:连接PE,
∵△ACP,△ADE都是等边三角形,
∴AC=AD=DE,AD=AE,∠CAP=∠DAE=60°,
∴∠CAD=∠PAE,
∴△CAD≌△PAE,
∴∠ACD=∠APE=90°,
∴EP⊥AB,∵PA=PB,
∴EA=EB,∵DE=AE,
∴ED=EB;
(3)当点D为边CB延长线上任意一点时,同法可证:ED=EB,
故答案为:ED=EB;
拓展应用:如图3中,作AH⊥x轴于H,CF⊥OB于F,连接OA,
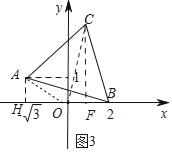
∵A(﹣![]() ,1),
,1),
∴∠AOH=30°,
由(2)可知,CO=CB,
∵CF⊥OB,
∴OF=FB=1,
∴可以假设C(1,n),
∵OC=BC=AB,
∴1+n2=1+(![]() +2)2,
+2)2,
∴n=2+![]() ,
,
∴C(1,2+![]() ).
).


科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
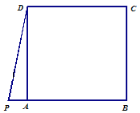
【题目】如图,正方形 ABCD 中,P 是 BA 延长线上一点,且PDA (0 45).点 A,点 E 关于 DP 对称,连接 ED,EP ,并延长 EP 交射线CB 于点 F ,连接 DF .
(1)请按照题目要求补全图形.
(2)求证:∠EDF=∠CDF
(3)求∠EDF(含有 的式子表示);
(4)过 P 做PH⊥DP交 DF 于点 H ,连接 BH , 猜想 AP 与 BH 的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
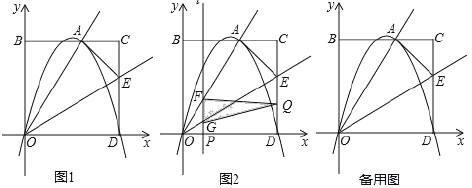
【题目】如图1,矩形OBCD的边OD,OB分别在x轴和y轴上,且B (0,8),D(10,0).点E是DC边上一点,将矩形OBCD沿过点O的射线OE折叠,使点D恰好落在BC边上的点A处.
(1)若抛物线y=ax2+bx经过点A,D,求此抛物线的解析式;
(2)若点M是(2)中抛物线对称轴上的一点,是否存在点M,使△AME为等腰三角形?若存在,直接写出点M的坐标;若不存在,说明理由;
(3)如图2,动点P从点O出发沿x轴正方向以每秒1个单位的速度向终点D运动,动点Q从点D出发沿折线D﹣C﹣A以同样的速度运动,两点同时出发,当一点运动到终点时,另一点也随之停止,过动点P作直线1⊥x轴,依次交射线OA,OE于点F,G,设运动时间为t(秒),△QFG的面积为S,求S与t的函数关系式,并直接写出t的取值范围.(t的取值应保证△QFG的存在)
查看答案和解析>>
科目:初中数学 来源: 题型:
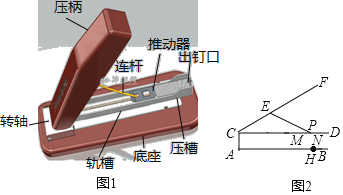
【题目】如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据:![]() ≈2.24,
≈2.24,![]() ≈6.08,sin53°≈0.80,cos53°≈0.60)
≈6.08,sin53°≈0.80,cos53°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.抛物线![]() 经过
经过![]() 三点.
三点.
(1)求抛物线的函数关系式;
(2)若直线![]() 是抛物线的对称轴,设点
是抛物线的对称轴,设点![]() 是直线
是直线![]() 上的一个动点,当
上的一个动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标;
的坐标;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得以线段
,使得以线段![]() 为直径的圆与边
为直径的圆与边![]() 交于
交于![]() 点(与点
点(与点![]() 不同),且以
不同),且以![]() 点为顶点的三角形是等腰三角形?若存在,求出
点为顶点的三角形是等腰三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC.
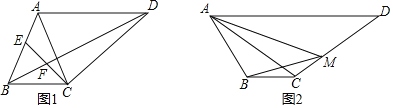
(1)如图1,AB=AC,点E为AB上一点,∠BEC=∠ACD.
①求证:ABBC=ADBE;
②连接BD交CE于F,试探究CF与CE的数量关系,并证明;
(2)如图2,若AB≠AC,点M在CD上,cos∠DAC=cos∠BMA=![]() ,AC=CD=3MC,ADBC=12,直接写出BC的长.
,AC=CD=3MC,ADBC=12,直接写出BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,点
,点![]() 是射线
是射线![]() 上一动点(不与
上一动点(不与![]() 点重合),过点
点重合),过点![]() 作直线
作直线![]() 的平行线交
的平行线交![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于
于![]() ,连结
,连结![]() ,
,![]() ,
,![]() .
.
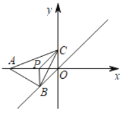
(1)当点![]() 在线段
在线段![]() 上且
上且![]() 时,
时,![]() __________.
__________.
(2)当![]() 与
与![]() 相似时,
相似时,![]() 点的横坐标为____________.
点的横坐标为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了![]() .
.
(1)已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?
(2)某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为![]() 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com