
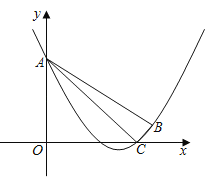
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
(1)求抛物线的表达式及点A的坐标;
(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠PAB=45°.求证:△PQA∽△ACB;
(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+5,点A坐标为(0,5);(2)详见解析;(3)
x+5,点A坐标为(0,5);(2)详见解析;(3)![]() .
.
【解析】
(1)将点B、C代入抛物线解析式y=![]() x2+mx+n即可;
x2+mx+n即可;
(2)先证△ABC为直角三角形,再证∠QAP+∠CAB=90°,又因∠AQP=∠ACB=90°,即可证△PQA∽△ACB;
(3)做点B关于AC的对称点B',求出BB'的坐标,直线AB'的解析式,即可求出点F'的坐标,接着求直线FF'的解析式,求出其与AB的交点即可.
解:(1)将B(6,1),C(5,0)代入抛物线解析式y=![]() x2+mx+n,
x2+mx+n,
得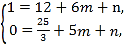
解得,m=﹣![]() ,n=5,
,n=5,
则抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x+5,点A坐标为(0,5);
x+5,点A坐标为(0,5);
(2)∵AC=![]() ,BC=
,BC=![]() ,AB=
,AB=![]() ,
,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠ACB=90°,
当∠PAB=45°时,点P只能在点B右侧,过点P作PQ⊥y 轴于点Q,
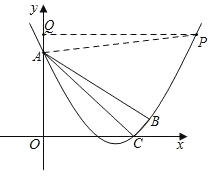
∴∠QAB+∠OAB=180°﹣∠PAB=135°,
∴∠QAP+∠CAB=135°﹣∠OAC=90°,
∵∠QAP+∠QPA=90°,∴∠QPA=∠CAB,
又∵∠AQP=∠ACB=90°,∴△PQA∽△ACB;
(3)做点B关于AC的对称点B',则A,F',B'三点共线,
由于AC⊥BC,根据对称性知点B'(4,﹣1),
将B'(4,﹣1)代入直线y=kx+5,
∴k=﹣![]() ,∴yAB'=﹣
,∴yAB'=﹣![]() x+5,
x+5,
联立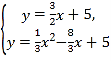 解得,x1=
解得,x1=![]() ,x2=0(舍去),
,x2=0(舍去),
则F'(![]() ,﹣
,﹣![]() ),
),
将B(6,1),B'(4,﹣1)代入直线y=mx+n,
得,![]() 解得,
解得,![]() ∴yBB'=x﹣5,
∴yBB'=x﹣5,
由题意知,kFF'=KBB',∴设yFF'=x+b,
将点F'(![]() ,﹣
,﹣![]() )代入,得,b=﹣
)代入,得,b=﹣![]() ,
,
∴yFF'=x﹣![]() ,
,
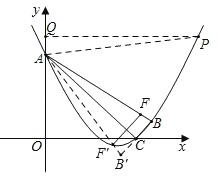
联立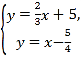 解得,
解得,
∴F(![]() ,
,![]() ),
),
则FF'=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)如图1,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,填空:当点
,填空:当点![]() 位于__________时,线段
位于__________时,线段![]() 的长取到最大值__________,且最大值为;(用含
的长取到最大值__________,且最大值为;(用含![]() 、
、![]() 的式子表示).
的式子表示).

(2)如图2,若点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 为边,作等边
为边,作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,
,![]() .
.

①图中与线段![]() 相等的线段是线段__________,并说明理由;
相等的线段是线段__________,并说明理由;
②直接写出线段![]() 长的最大值为__________.
长的最大值为__________.
(3)如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 长的最大值为__________,及此时点
长的最大值为__________,及此时点![]() 的坐标为__________.(提示:等腰直角三角形的三边长
的坐标为__________.(提示:等腰直角三角形的三边长![]() 、
、![]() 、
、![]() 满足
满足![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
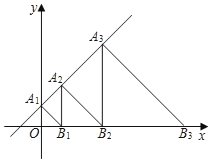
【题目】如图,直线L:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交L于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交L于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2019等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,某校开设了“3D”打印、数学编程、智能机器人、陶艺制作“四门创客课程记为A、B、C、D,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成两幅均不完整的统计图表:
创客课程 | 频数 | 频率 |
“3D”打印 | 36 | 0.45 |
数学编程 | 0.25 | |
智能机器人 | 16 | b |
陶艺制作 | 8 | |
合计 | a | 1 |
请根据图表中提供的信息回答下列问题:
(1)统计表中的a=______,b=______;
(2)“陶艺制作”对应扇形的圆心角为______;
(3)根据调查结果,请你估计该校300名学生中最喜欢“智能机器人”创客课程的人数;
(4)学校为开设这四门课程,预计每生A、B、C、D四科投资比为4:3:6:7,若“3D打印课程每人投资200元,求学校为开设创客课程,需为学生人均投入多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
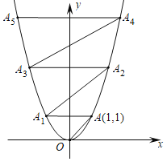
【题目】在平面直角坐标系中,抛物线y=x2的图象如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2019的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C
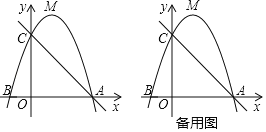
(1)求抛物线的表达式;
(2)在直线AC的上方的抛物线上,有一点P(不与点M重合),使△ACP的面积等于△ACM的面积,请求出点P的坐标;
(3)在y轴上是否存在一点Q,使得△QAM为直角三角形?若存在,请直接写出点Q的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳能是来自太阳的辐射能量,对于地球上的人类来说,太阳能是对环境无任何污染的可再生能源,因此许多国家都在大陆发展太阳能.如图是2013-2017年我国光伏发电装机容量统计图.根据统计图提供的信息,判断下列说法不合理的是( )
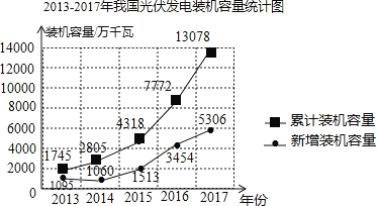
A.截至2017年底,我国光伏发电累计装机容量为13078万千瓦
B.2013-2017年,我国光伏发电新增装机容量逐年增加
C.2013-2017年,我国光伏发电新增装机容量的平均值约为2500万千瓦
D.2017年我国光伏发电新增装机容量大约占当年累计装机容量的40%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com