
【题目】如图,已知CD⊥AB于点D,BE⊥AC于点E,CD、BE交于点O,且AO平分∠BAC,则图中的全等三角形共有( )
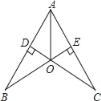
A. 1对 B. 2对 C. 3对 D. 4对
【答案】D
【解析】
共有四对.分别为△ADO≌△AEO,△ADC≌△AEB,△ABO≌△ACO,△BOD≌△COE.做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找.
解答:解:∵CD⊥AB,BE⊥AC,AO平分∠BAC
∴∠ADO=∠AEO=90°,∠DAO=∠EAO
∵AO=AO
∴△ADO≌△AEO;(AAS)
∴OD=OE,AD=AE
∵∠DOB=∠EOC,∠ODB=∠OEC=90°
∴△BOD≌△COE;(ASA)
∴BD=CE,OB=OC,∠B=∠C
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°
∴△ADC≌△AEB;(ASA)
∵AD=AE,BD=CE
∴AB=AC
∵OB=OC,AO=AO
∴△ABO≌△ACO.(SSS)
所以共有四对全等三角形.
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.
(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
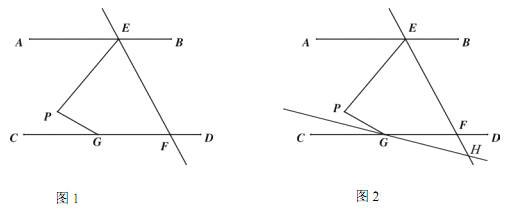
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于下列各组条件,不能判定△![]() ≌△
≌△![]() 的一组是 ( )
的一组是 ( )
A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方案设计题)如图是人民公园中的荷花池,现要测量荷花池岸边树A与树B间的距离.如果直接测量比较困难,请你根据所学知识,以卷尺和测角仪为测量工具,设计两种不同的测量方案并画出图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
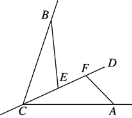
【题目】如图,已知CA=CB,点E,F在射线CD上,满足∠BEC=∠CFA,且∠BEC+∠ECB+∠ACF=180°.
(1)求证:△BCE≌△CAF;
(2)试判断线段EF,BE,AF的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问 ![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com