
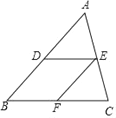
【题目】如图,在△ABC中,D是AB中点,E是AC中点,F是BC中点,请填空:
(1)四边形BDEF是 四边形;
(2)若四边形BDEF是菱形,则△ABC满足的条件是 .
(3)若四边形BDEF是矩形,则△ABC满足的条件是 .
(4)若四边形BDEF是正方形,则△ABC满足的条件是 .
并就(2)、(3)、(4)中选取一个进行证明.
【答案】(1)平行;(2)AB=BC;(3)∠B=90°;(4)∠B=90°,AB=BC
【解析】
(1)根据三角形的中位线定理和平行四边形的判定解答即可;
(2)根据菱形的判定解答即可;
(3)根据矩形的判定解答即可;
(4)根据正方形的判定解答即可.
(1)∵在△ABC中,D是AB中点,E是AC中点,F是BC中点,∴DE∥BC,EF∥AB,∴四边形BDEF是平行四边形.
故答案为:平行;
(2)当AB=BC时,∴BD=BF,∴平行四边形BDEF是菱形.
故答案为:AB=BC;
(3)当∠B=90°时,∴平行四边形BDEF是矩形.
故答案为:;∠B=90°;
(4)当∠B=90°,AB=BC,∴平行四边形BDEF是正方形.
故答案为:∠B=90°,AB=BC.


科目:初中数学 来源: 题型:
【题目】某市政部门为了保护生态环境,计划购买A,B两种型号的环保设备.已知购买一套A型设备和三套B型设备共需230万元,购买三套A型设备和两套B型设备共需340万元.
(1)求A型设备和B型设备的单价各是多少万元;
(2)根据需要市政部门采购A型和B型设备共50套,预算资金不超过3000万元,问最多可购买A型设备多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G、交BC的延长线于H,则以下结论:①DE=DG;②BE=CG;③DF=DB;(④BH=CF.其中正确的是____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(或方程组)解应用题2019年是决胜全面建成小康社会、打好污染防治攻坚战的关键之年.为了解决垃圾回收最后一公里的难题,“小黄狗”智能垃圾分类回收环保公益项目通过大数据、人工智能和物联网等先进科技进驻小区、写字楼、学校、机关和社区等进行回收.某位小区居民装修房屋,在过去的一个月内投放纸类垃圾和塑料垃圾共82公斤,其中纸类垃圾的投放是塑料垃圾的8倍多10公斤,请问这位小区居民在过去的一个月内投放纸类垃圾和塑料垃圾分别是多少公斤?

查看答案和解析>>
科目:初中数学 来源: 题型:
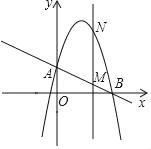
【题目】如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.
(1)求该抛物线的解析式和顶点坐标;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:有理数a、b、c在数轴上的位置如图所示,且|c|>|a|.
![]()
(1)若|a+10|=20,b2=400,c的相反数是30,求a、b、c的值;
(2)在(1)的条件下,a、b、c分别是A、B、C点在数轴上所对应的数,
①线段AC的长是________,将数轴折叠使得点A和点C重合,则折痕处在数轴上表示的数是__________
②数轴上是否存在一点P,使得P点到C点的距离加上P点到A点的距离减去P点到B点的距离为50,即PC+PAPB=50?若存在,求出P点在数轴上所对应的数;若不存在,请说明理由;
③点C,B分别以4个单位/秒和3个单位/秒的速度同时向右运动,点A以7个单位/秒的速度向右运动,是否存在常数m,使得3CA+2mOB-mOA为定值,若存在,请求出m值以及这个定值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
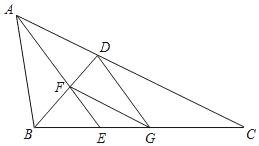
【题目】如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD相交于点F,FG∥AC,联结DG.
(1)求证:BFBC=ABBD;
(2)求证:四边形ADGF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com