
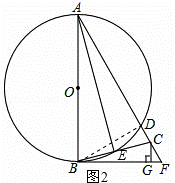
如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O于点E,且∠BAF=2∠CBF,CG⊥BF于点G,连接AE.
(1)直接写出AE与BC的位置关系;
(2)求证:△BCG∽△ACE;
(3)若∠F=60°,GF=1,求⊙O的半径长.
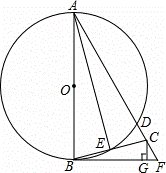
解:(1)如图1,
∵AB是⊙O的直径,
∴∠AEB=90°.
∴AE⊥BC.
(2)如图1,
∵BF与⊙O相切,
∴∠ABF=90°.
∴∠CBF=90°﹣∠ABE=∠BAE.
∵∠BAF=2∠CBF.
∴∠BAF=2∠BAE.
∴∠BAE=∠CAE.
∴∠CBF=∠CAE.
∵CG⊥BF,AE⊥BC,
∴∠CGB=∠AEC=90°.
∵∠CBF=∠CAE,∠CGB=∠AEC,
∴△BCG∽△ACE.
(3)连接BD,如图2所示.
∵∠DAE=∠DBE,∠DAE=∠CBF,
∴∠DBE=∠CBF.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴BD⊥AF.
∵∠DBC=∠CBF,BD⊥AF,CG⊥BF,
∴CD=CG.
∵∠F=60°,GF=1,∠CGF=90°,
∴tan∠F=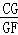 =CG=tan60°=
=CG=tan60°=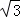
∵CG=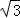 ,
,
∴CD=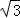 .
.
∵∠AFB=60°,∠ABF=90°,
∴∠BAF=30°.
∵∠ADB=90°,∠BAF=30°,
∴AB=2BD.
∵∠BAE=∠CAE,∠AEB=∠AEC,
∴∠ABE=∠ACE.
∴AB=AC.
设⊙O的半径为r,则AC=AB=2r,BD=r.
∵∠ADB=90°,
∴AD=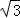 r.
r.
∴DC=AC﹣AD=2r﹣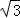 r=(2﹣
r=(2﹣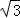 )r=
)r=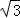 .
.
∴r=2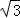 +3.
+3.
∴⊙O的半径长为2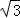 +3.
+3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com