
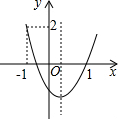
 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由抛物线的开口方向判断a的取值,由抛物线与y轴的交点判断c的取值,然后根据对称轴的位置确定b的符号;
②根据对称轴x=-$\frac{b}{2a}$<1,进行判断;
③将(-1,2)和点(1,0)代入二次函数y=ax2+bx+c中,进行整理可得结论;
④由③中的两个等式相减可得结论.
解答 解:①∵抛物线的开口向上,
∴a>0,
∵对称轴在y轴右侧,
∴a、b异号,
∴b<0,
∵抛物线与y轴的交点在y轴的负半轴上,
∴c<0,故abc>0;
所以①不正确;
②由图象可知:对称轴x=-$\frac{b}{2a}$>0且对称轴x=-$\frac{b}{2a}$<1,
∵a>0,
∴-b<2a,
∴2a+b>0,
∴4a+b>0;
所以②正确;
③由题意可知:当x=-1时,y=2,
∴a-b+c=2,
当x=1时,y=0,
∴a+b+c=0,
a-b+c=2与a+b+c=0相加得2a+2c=2,即a+c=1,
所以③正确;
④∵a+c=1,
∴移项得c=1-a,
又∵a>0,c<0,
∴a>1,
由$\left\{\begin{array}{l}{a+b+c=0}\\{a-b+c=2}\end{array}\right.$得:b=-1,
∴a-b>1-b,
∴a-b>2,
所以④不正确;
所以本题正确的有:②③,两个;
故选B.
点评 本题考查了二次函数图象与系数的关系,要做好此类题,要明确以下几点:
(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0.
(2)b由对称轴和a的符号确定;
(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.
(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
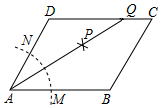 如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为15.
如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
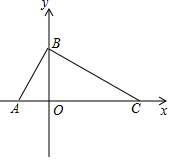 如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.
如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以对角线OA2为边作正方形OA2A3B2,…,依此规律,点A2017的坐标是(21008,21008).
如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以对角线OA2为边作正方形OA2A3B2,…,依此规律,点A2017的坐标是(21008,21008).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
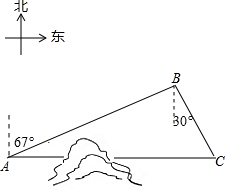 如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向.若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向.若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com