
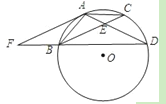
【题目】如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=![]() ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=![]() BD,连接AF.
BD,连接AF.
(1)证明:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E为边上一点,连结AE并延长交直线DC于F,且CE=CF.
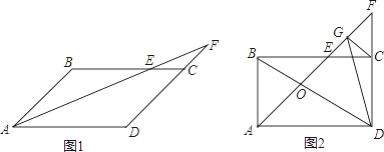
(1)如图1,求证:AF是∠BAD的平分线;
(2)如图2,若∠ABC=90°,点G是线段EF上一点,连接DG、BD、CG,若∠BDG=45°,求证:CG=![]() EF.
EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题用适当的方法解下列方程
(1)(3x﹣1)(4x+5)=0
(2)4x2﹣8x﹣3=0(配方法)
(3)x(x+1)=3x+6
(4)(x﹣2)(x+4)=16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝新中国成立70周年,某校组织八年级全体学生参加“恰同学少年,忆峥嵘岁月”新中国成立70周年知识竞赛活动.将随机抽取的部分学生成绩进行整理后分成5组,50~60分(![]() )的小组称为“学童”组,60~70分(
)的小组称为“学童”组,60~70分(![]() )的小组称为“秀才”组,70~80分(
)的小组称为“秀才”组,70~80分(![]() )的小组称为“举人”组,80~90分(
)的小组称为“举人”组,80~90分(![]() )的小组称为“进士”组,90~100分(
)的小组称为“进士”组,90~100分(![]() )的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
)的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
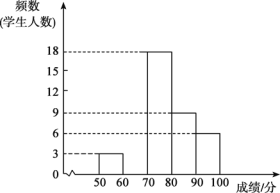
(1)若“翰林”组成绩的频率是12.5%,请补全频数分布直方图;
(2)在此次比赛中,抽取学生的成绩的中位数在 组;
(3)学校决定对成绩在70~100分(![]() )的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
)的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是半径为![]() cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.
cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.
(1)求△PDE的周长;
(2)若DE=![]() cm,求图中阴影部分的面积.
cm,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与○O相交于点D,连接BD,则∠DBC的大小为

A. 15° B. 35° C. 25° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆针旋转90°,点B旋转到点C的位置,一条抛物找正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点D,分别过点P,点D作x轴的垂线,交x轴于R,S两点,问:四边形PRSD的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如图2,把点B向下平移两个单位得到点T,过O,T两点作⊙Q交x轴,y轴于E,F两点,若M、N分别为弧![]() 、
、![]() 的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
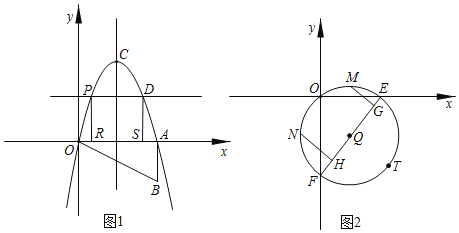
查看答案和解析>>
科目:初中数学 来源: 题型:
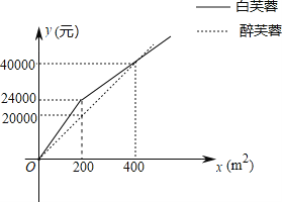
【题目】2019车8月8日至18日,第十八届“世警会”首次来到亚洲在成都举办武侯区以相关事宜为契机,进一步改善区域生态环境.在天府吴园道部分地段种植白芙蓉和醉芙蓉两种花卉.经市场调查,种植费用y(元)与种植面积x(m2)之间的函数关系如图所示.
(1)请直接写出两种花卉y与x的函数关系式;
(2)白芙蓉和醉芙蓉两种花卉的种植面积共1000m2,若白芙蓉的种植面积不少于100m2且不超过醉芙蓉种植面积的3倍,那么应该怎样分配两种花卉的种植面积才能使种植总费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com