
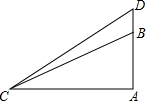
 如图,△ABC中,∠A=90°,AC=20,AB=10,延长AB到D,使AC+AB=CD+BD,求BD的长.
如图,△ABC中,∠A=90°,AC=20,AB=10,延长AB到D,使AC+AB=CD+BD,求BD的长.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $y=\frac{x}{3}$ | B. | y=$\frac{1}{x+1}$ | C. | y=$\frac{1}{2}$x | D. | y=$\frac{1}{3x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
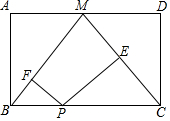 如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,垂足分别为E,F,当AB,BC满足什么条件时,四边形PEMF为矩形?试加以证明.
如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,垂足分别为E,F,当AB,BC满足什么条件时,四边形PEMF为矩形?试加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
| 摸到黑球的频率$\frac{m}{n}$ | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
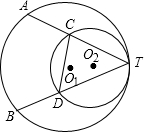 已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.
已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com