
 如图,∠AOB=60°,点E在∠AOB的平分线上,EC⊥OA,且CE=1,点D是OB上的一个动点,当ED取最小值时,线段CD的长度为$\sqrt{3}$.
如图,∠AOB=60°,点E在∠AOB的平分线上,EC⊥OA,且CE=1,点D是OB上的一个动点,当ED取最小值时,线段CD的长度为$\sqrt{3}$. 分析 作ED⊥OB于D,连接CD,根据直角三角形的性质求出OC,证明Rt△OCE≌Rt△ODE,得到OC=OD,证明△COD是等边三角形,根据等边三角形的性质解答.
解答 解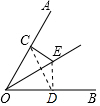 :作ED⊥OB于D,连接CD,
:作ED⊥OB于D,连接CD,
∵点E在∠AOB的平分线上,EC⊥OA,ED⊥OB,
∴DE=CE,∠AOE=30°,
∵OC=$\sqrt{3}$,
在Rt△OCE和Rt△ODE中,
$\left\{\begin{array}{l}{CE=DE}\\{OE=OE}\end{array}\right.$,
∴Rt△OCE≌Rt△ODE,
∴OC=OD,又∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查的是角平分线的性质、全等三角形的判定和性质、等边三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
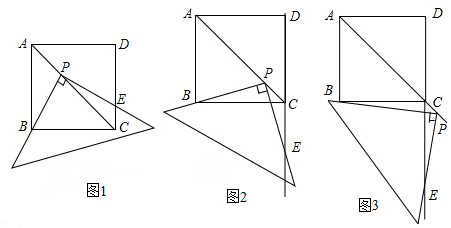
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
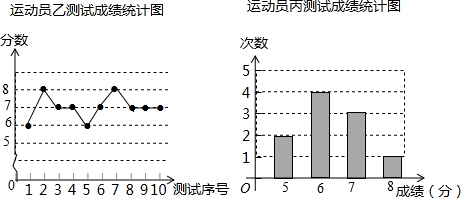
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
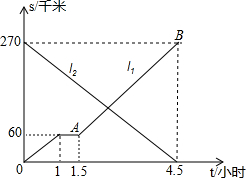 一辆车和一辆货车分别从甲,乙两地相向而行,图中的l1,l2分别表示轿车和货车离甲地的路程s(千米)与行驶时间t(小时)间的关系.
一辆车和一辆货车分别从甲,乙两地相向而行,图中的l1,l2分别表示轿车和货车离甲地的路程s(千米)与行驶时间t(小时)间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
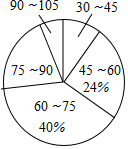 为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:
为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:| 课外作业时间 (分组) | 人数 (频数) |
| 30~45 | 5 |
| 45~60 | 12 |
| 60~75 | a |
| 75~90 | 10 |
| 90~105 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
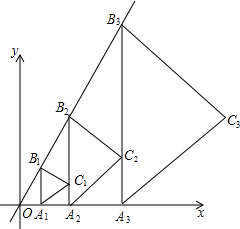 如图,点A1(1,0)在x轴上,过点A1作A1B1∥y轴交直线y=$\sqrt{3}$x于点B1,以A1B1为边在A1B1的右侧作等边△A1B1C1,再过点C1作A2B2∥y轴,分别交直线x轴和直线y=$\sqrt{3}$x于A2,B2两点,再以A2B2为边在A2B2的右侧作等边△A2B2C2…,按此规律进行下去,则等边△AnBnCn的面积为$\frac{\sqrt{3}}{4}$[$(\frac{5}{2})^{n-1}$•$\sqrt{3}$]2(用含正整数n的代数式表示).
如图,点A1(1,0)在x轴上,过点A1作A1B1∥y轴交直线y=$\sqrt{3}$x于点B1,以A1B1为边在A1B1的右侧作等边△A1B1C1,再过点C1作A2B2∥y轴,分别交直线x轴和直线y=$\sqrt{3}$x于A2,B2两点,再以A2B2为边在A2B2的右侧作等边△A2B2C2…,按此规律进行下去,则等边△AnBnCn的面积为$\frac{\sqrt{3}}{4}$[$(\frac{5}{2})^{n-1}$•$\sqrt{3}$]2(用含正整数n的代数式表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com