
【题目】如图,抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,且与
,且与![]() 轴相交于A,B两点(点B在点A的右侧),与
轴相交于A,B两点(点B在点A的右侧),与![]() 轴交于点C.
轴交于点C.
(1)求抛物线的解析式和A,B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B,C重合),则是否存在一点P,使△BPC的面积最大?若存在,请求出△BPC的最大面积;若不存在,试说明理由.

【答案】(1)![]() ,点A的坐标为(-2,0),点B的坐标为(8,0);(2)当
,点A的坐标为(-2,0),点B的坐标为(8,0);(2)当![]() =4时,△PBC的面积最大,最大面积是16.
=4时,△PBC的面积最大,最大面积是16.
【解析】
(1)由抛物线的对称轴是直线x=3,解出a的值,即可求得抛物线解析式,在令其y值为0,解一元二次方程即可求出A和B的坐标;
(2)易求点C的坐标为(0,4),设直线BC的解析式为y=kx+b(k≠0),将B(8,0),C(0,4)代入y=kx+b,解出k和b的值,即得直线BC的解析式;设点P的坐标为(![]() ,
,![]() ),过点P作PD∥y轴,交直线BC于点D,则点D的坐标为(
),过点P作PD∥y轴,交直线BC于点D,则点D的坐标为(![]() ,
,![]() ),利用面积公式得出关于x的二次函数,从而求得其最值.
),利用面积公式得出关于x的二次函数,从而求得其最值.
(1)∵抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,
,
∴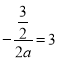 ,解得
,解得![]() ,
,
∴ 抛物线的解析式为:![]() ,
,
当![]() 时,即
时,即![]() ,
,
解之得:![]() ,
,![]() ,
,
∴点A的坐标为(-2,0),点B的坐标为(8,0),
故答案为:![]() ,点A的坐标为(-2,0),点B的坐标为(8,0);
,点A的坐标为(-2,0),点B的坐标为(8,0);
(2)当![]() 时,
时,![]()
∴点C的坐标为(0,4)
设直线BC的解析式为![]() ,
,
将点B(8,0)和点C(0,4)的坐标代入![]() 得:
得:
![]() ,
,
解之得: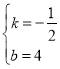 ,
,
∴直线BC的解析式为![]() ,
,
假设存在,
设点P 的坐标为(![]() ,
,![]() ),
),
过点P作PD∥![]() 轴,交直线BC于点D,交
轴,交直线BC于点D,交![]() 轴于点E,
轴于点E,
则点D的坐标为(![]() ,
,![]() ),如图所示,
),如图所示,

PD=![]() -(
-(![]() )=
)=![]()
∴S△PBC=S△PDC+ S△PDB=![]()
=![]()
=![]()
=![]()
∵-1<0
∴当![]() =4时,△PBC的面积最大,最大面积是16.
=4时,△PBC的面积最大,最大面积是16.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x(x﹣3)(0≤x≤3)的图象,记为C1,它与x轴交于点O,A1;将C1点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……若P(2020,m)在这个图象连续旋转后的所得图象上,则m=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
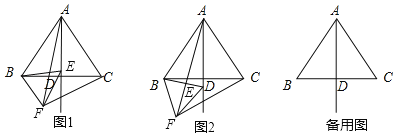
【题目】已知△ABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转60°得到BF,连接EF、CF、AF.
(1)如图1,当点E在线段AD上时,猜想∠AFC和∠FAC的数量关系;(直接写出结果)
(2)如图2,当点E在线段AD的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点E在直线AD上运动,当△ACF是等腰直角三角形时,请直接写出∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①4a+2b<0;
②﹣1≤a≤![]() ;
;
③对于任意实数m,a+b≥am2+bm总成立;
④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
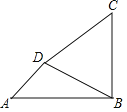
【题目】如图,海中有两个小岛![]() ,
,![]() ,某渔船在海中的
,某渔船在海中的![]() 处测得小岛D位于东北方向上,且相距
处测得小岛D位于东北方向上,且相距![]() ,该渔船自西向东航行一段时间到达点
,该渔船自西向东航行一段时间到达点![]() 处,此时测得小岛
处,此时测得小岛![]() 恰好在点
恰好在点![]() 的正北方向上,且相距
的正北方向上,且相距![]() ,又测得点
,又测得点![]() 与小岛
与小岛![]() 相距
相距![]() .
.
(1)求![]() 的值;
的值;
(2)求小岛![]() ,
,![]() 之间的距离(计算过程中的数据不取近似值).
之间的距离(计算过程中的数据不取近似值).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果按此速度增涨,该公司六月份的快递件数将达到多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B点测得C点的仰角为60°.已知AB=20m,点C和直线AB在同一铅垂平面上,求气球离地面的高度(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com