
【题目】如图所示,⊙O中,弦AC、BD交于E,![]() .
.
(1)求证:![]() ;
;
(2)延长EB到F,使EF=CF,试判断CF与⊙O的位置关系,并说明理由.
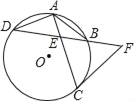
【答案】(1)详见解析;(2)CF与⊙O相切,理由详见解析.
【解析】
(1)连接BC,由![]() =2
=2![]() ,得
,得![]() =
=![]() ,则∠ABD=∠ACB,得到△ABE∽△ABC,所以AB2=AEAC;
,则∠ABD=∠ACB,得到△ABE∽△ABC,所以AB2=AEAC;
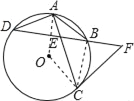
(2)连接AO、CO,由A为![]() 中点,得到AO⊥DB,得到∠OAC+∠AED=90°,所以∠OAC+∠FEC=90°,而EF=CF,则∠FEC=∠ECF,又∠OAC=∠OCA,所以∠OAC+∠FEC=∠OCA+∠ECF=90°,即得到CF与⊙O相切.
中点,得到AO⊥DB,得到∠OAC+∠AED=90°,所以∠OAC+∠FEC=90°,而EF=CF,则∠FEC=∠ECF,又∠OAC=∠OCA,所以∠OAC+∠FEC=∠OCA+∠ECF=90°,即得到CF与⊙O相切.
证明:(1)连接BC,如图,
∵![]() =2
=2![]() .
.
∴![]() =
=![]() .
.
∴∠ABD=∠ACB,
而∠CAB公用,
∴△ABE∽△ABC,
∴![]()
∴![]()
(2)CF与⊙O相切.理由如下:
连接AO、CO,
∵A为![]() 中点,
中点,
∴AO⊥DB,
∴∠OAC+∠AED=90°
∵∠AED=∠FEC,
∴∠OAC+∠FEC=90°,
又∵EF=CF,
∴∠FEC=∠ECF,
∵AO=OC,
∴∠OAC=∠OCA,
∴∠OAC+∠FEC=∠OCA+∠ECF=90°,
∴FC与⊙O相切.


科目:初中数学 来源: 题型:
【题目】如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证
(1)∠AHO=90°
(2)求证:CH=AHOH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
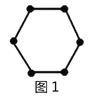
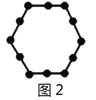
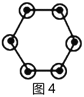
例如:图1有6个点,图2有12个点,图3有18个点,…,按此规律,求图8、图![]() 有多少个点?
有多少个点?
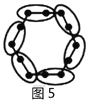
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是![]() 个;图2中黑点个数是
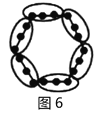
个;图2中黑点个数是![]() 个;图3中黑点个数是
个;图3中黑点个数是![]() 个;…,所以容易求出图8、图
个;…,所以容易求出图8、图![]() 中黑点的个数分别是______、_________.
中黑点的个数分别是______、_________.

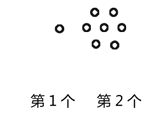
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第6个点阵中有______个圆圈;第![]() 个点阵中有______个圆圈.
个点阵中有______个圆圈.
(2)小圆圈的个数会等于331吗?请求出是第几个点阵.


查看答案和解析>>
科目:初中数学 来源: 题型:
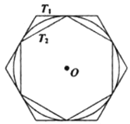
【题目】如图,有一个圆![]() 和两个正六边形
和两个正六边形![]() ,
,![]() .
.![]() 的6个顶点都在圆周上,
的6个顶点都在圆周上,![]() 的6条边都和圆
的6条边都和圆![]() 相切(我们称
相切(我们称![]() ,
,![]() 分别为圆
分别为圆![]() 的外切正六边形和内接正六边形),若设
的外切正六边形和内接正六边形),若设![]() ,
,![]() 的周长分别为
的周长分别为![]() ,
,![]() ,圆
,圆![]() 的半径为
的半径为![]() ,则
,则![]() ___;
___;![]() ____;正六边形
____;正六边形![]() ,
,![]() 的面积比
的面积比![]() 的值是____.
的值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中,
中,![]() ,将扇形
,将扇形![]() 按图1摆放,使扇形的半径
按图1摆放,使扇形的半径![]() 、
、![]() 分别与
分别与![]() 、
、![]() 重合,
重合,![]() .
.
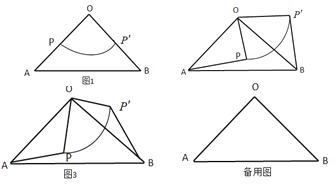
如图2,若![]() 不动,让扇形
不动,让扇形![]() 绕点
绕点![]() 逆时针旋转一周,连接线段
逆时针旋转一周,连接线段![]() 、
、![]() ,设旋转角为
,设旋转角为![]() .
.
发现:直接写出![]() 、
、![]() 的数量关系.
的数量关系.
探究:若![]()
(1)扇形![]() 绕到点
绕到点![]() 的左侧,当
的左侧,当![]() 时,旋转角
时,旋转角![]() ______°;
______°;
(2)扇形![]() 绕到点
绕到点![]() 的右侧,当
的右侧,当![]() 与
与![]() 相切时,求
相切时,求![]() ;
;
(3)若点![]() 是弧
是弧![]() 上任意一点,在扇形
上任意一点,在扇形![]() 绕点
绕点![]() 逆时针转过程中,当
逆时针转过程中,当![]() 的面积最大时,直接写出
的面积最大时,直接写出![]() 的度数;
的度数;
延伸:如图3,若![]() ,当
,当![]() 、
、![]() 、
、![]() 三点共线时,直接写出线段
三点共线时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,点
,点![]() 是第一象限抛物线上的点,连结
是第一象限抛物线上的点,连结![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐为
的横坐为![]() ,
,![]() 与
与![]() 的比值为
的比值为![]() .
.
(1)![]() __________;
__________;
(2)当![]() 取最大值时,
取最大值时,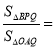 __________.
__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
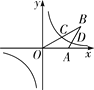
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)的图象经过等腰△AOB底边OB的中点C和AB边上一点D,已知A(4,0),∠AOB=30°,则k的值为( )
(k≠0)的图象经过等腰△AOB底边OB的中点C和AB边上一点D,已知A(4,0),∠AOB=30°,则k的值为( )
A.2![]() B.3
B.3![]() C.3D.4
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
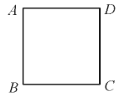
【题目】数学课上,王老师让同学们对给定的正方形![]() ,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
乙同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
丙同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
丁同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,分别过点![]() ,
,![]() 作
作![]() 轴的垂线
轴的垂线![]() 和
和![]() ,探究直线
,探究直线![]() 和
和![]() 与双曲线
与双曲线 ![]() 的关系,下列结论中错误的是
的关系,下列结论中错误的是
A.两直线中总有一条与双曲线相交
B.当![]() =1时,两条直线与双曲线的交点到原点的距离相等
=1时,两条直线与双曲线的交点到原点的距离相等
C.当![]() 时,两条直线与双曲线的交点在
时,两条直线与双曲线的交点在![]() 轴两侧
轴两侧
D.当两直线与双曲线都有交点时,这两交点的最短距离是2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com