
分析 (1)欲证明方程有两个不相等的实数根,只要证明△>0即可.
(2)①利用因式分解法求出方程的根即可解决问题.
②把①中的x1,x2代入已知条件,即可解决问题.
解答 (1)证明:∵△=[-(4k+1)]2-4k(3k+3)=4k2-4k+1=(2k-1)2
∵k是整数,∴k$≠\frac{1}{2}$,
∴△>0,
∴方程有两个不相等的实数根.
(2)解:①∵kx2-(4k+1)x+3k+3=0,
∴(x-3)[kx-(k+1)]=0,
∵x1<x2
∴x2=3,x1=$\frac{k+1}{k}$.
②∵m=x2-x1-2,
∴m=3-$\frac{k+1}{k}$-2,
∴m=1-$\frac{k+1}{k}$,
∴mk=k-k-1=-1.
点评 本题考查根与系数的关系,根的判别式等知识,解题的关键是灵活应用这些知识解决问题,学会整体代入的思想解决问题,属于中考常考题型.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数 | B. | 方差 | C. | 平均数 | D. | 中位数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{24}$ | D. | $\sqrt{0.3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $\frac{x+y}{y-x}$ | D. | $\frac{x+y}{x-y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省江阴市周庄学区九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
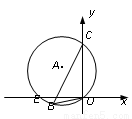
如图,⊙A经过点E、B、C、O,且C(0,8),E( 6,0),O(0,0),则cos∠OBC的值为( )
6,0),O(0,0),则cos∠OBC的值为( )
A.  B.
B.  C.
C.  D.
D. 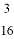
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com