
| A. | 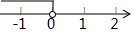 | B. |  | C. | 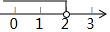 | D. |  |
科目:初中数学 来源: 题型:解答题
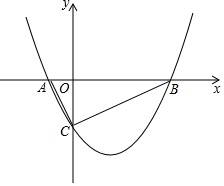 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴相交于点A、B,与y轴相交于点C,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴相交于点A、B,与y轴相交于点C,且A(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=BC | B. | AC⊥BD | C. | OA=OC | D. | AC平分∠BAD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
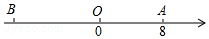
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
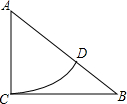 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若 AC=3,BC=4.则BD的长是( )
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若 AC=3,BC=4.则BD的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
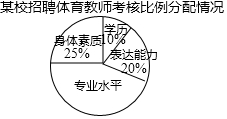 为贯彻国务院办公厅发布的《中国足球发展改革总体方案》精神,某校准备招聘一名足球专业的体育老师,该校对甲、乙、丙三名应聘者从学历、专业水平、身体素质、表达能力等四个方面考核打分,每一方面满分10分,得分情况如下表(单位:分),考核比例分配情况见扇形统计图.
为贯彻国务院办公厅发布的《中国足球发展改革总体方案》精神,某校准备招聘一名足球专业的体育老师,该校对甲、乙、丙三名应聘者从学历、专业水平、身体素质、表达能力等四个方面考核打分,每一方面满分10分,得分情况如下表(单位:分),考核比例分配情况见扇形统计图.| 甲 | 乙 | 丙 | |
| 学历 | 8 | 9 | 8 |
| 专业水平 | 9 | 8 | 9 |
| 身体素质 | 8 | 7 | 6 |
| 表达能力 | 7 | 8 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
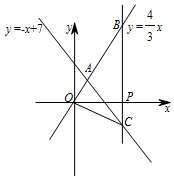 如图:在平面直角坐标系xOy中,已知正比例函数$y=\frac{4}{3}x$与一次函数y=-x+7的图象交于点A.
如图:在平面直角坐标系xOy中,已知正比例函数$y=\frac{4}{3}x$与一次函数y=-x+7的图象交于点A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com