
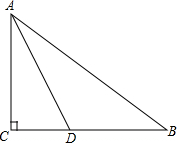
 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.分析 (1)作AD的垂直平分线交AC于O,以AO为半径画圆O分别交AB、AC于点E、F,则⊙O即为所求;
(2)连结OD,得到OD=OA,根据等腰三角形的性质得到∠OAD=∠ODA,等量代换得到∠ODA=∠CAD,根据平行线的判定定理得到OD∥AC,根据平行线的性质即可得到结论;
(3)连接DE,根据圆周角定理得到∠ADE=90°,根据三角形的内角和得到∠AOD=120°,根据三角函数的定义得到AE=$\frac{AD}{cos∠EAD}$=4,根据弧长个公式即可得到结论.
解答 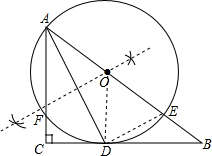 (1)解:如图所示,
(1)解:如图所示,
(2)证明:连结OD,则OD=OA,
∴∠OAD=∠ODA,
∵∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
即BC⊥OD,
∴BC与⊙O相切;
(3)解:连接DE,
∵AE是⊙O的直径,
∴∠ADE=90°,
∵∠OAD=∠ODA=30°,
∴∠AOD=120°,在
Rt△ADE中,
AE=$\frac{AD}{cos∠EAD}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4,
∴⊙O的半径=2,
∴劣弧AD的长=$\frac{120•π×2}{180}$=$\frac{4}{3}$π.
点评 本题考查了切线的判定,圆周角定理,解直角三角形,弧长的计算,平行线的判定,基本作图,作出辅助线构建直角三角形是本题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,则下列说法正确的是( )
如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,则下列说法正确的是( )| A. | 甲比乙的成绩稳定 | B. | 乙比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定谁的成绩更稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形纸片ABCD,AB=$\sqrt{3}$,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
如图,矩形纸片ABCD,AB=$\sqrt{3}$,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
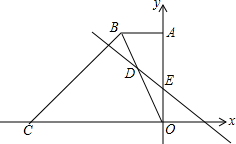 如图,直角梯形OABC的顶点C,A分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠OCB=45°,BC=6$\sqrt{2}$,直线DE交OB于点D,交y轴于点E,OD=2BD,且OE,OC的长分别为方程x2-11x+18=0的两个根(OE<OC).
如图,直角梯形OABC的顶点C,A分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠OCB=45°,BC=6$\sqrt{2}$,直线DE交OB于点D,交y轴于点E,OD=2BD,且OE,OC的长分别为方程x2-11x+18=0的两个根(OE<OC).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com