
【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y= ![]() x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.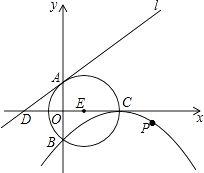
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.
【答案】
(1)
解:如图1,连接AE,由已知得:AE=CE=5,OE=3,
在Rt△AOE中,由勾股定理得,OA= ![]() =
= ![]() =4,
=4,
∵OC⊥AB,
∴由垂径定理得,OB=OA=4,
OC=OE+CE=3+5=8,
∴A(0,4),B(0,﹣4),C(8,0),
∵抛物线的顶点为C,
∴设抛物线的解析式为y=a(x﹣8)2,
将点B的坐标代入上解析的式,得64a=﹣4,故a=﹣ ![]() ,
,
∴y=﹣ ![]() (x﹣8)2,
(x﹣8)2,
∴y=﹣ ![]() x2+x﹣4为所求抛物线的解析式
x2+x﹣4为所求抛物线的解析式
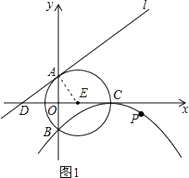
(2)
解:在直线l的解析式y= ![]() x+4中,令y=0,得
x+4中,令y=0,得 ![]() x+4=0,解得x=﹣
x+4=0,解得x=﹣ ![]() ,
,
∴点D的坐标为(﹣ ![]() ,0),
,0),
当x=0时,y=4,
∴点A在直线l上,
在Rt△AOE和Rt△DOA中,
∵ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵∠AOE=∠DOA=90°,
∴△AOE∽△DOA,
∴∠AEO=∠DAO,
∵∠AEO+∠EAO=90°,
∴∠DAO+∠EAO=90°,即∠DAE=90°,因此,直线l与⊙E相切与A
(3)
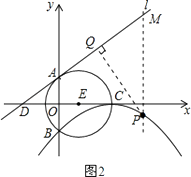
解:如图2,过点P作直线l的垂线段PQ,垂足为Q,过点P作直线PM垂直于x轴,交直线l于点M.
设M(m, ![]() m+4),P(m,﹣
m+4),P(m,﹣ ![]() m2+m﹣4),则
m2+m﹣4),则
PM= ![]() m+4﹣(﹣
m+4﹣(﹣ ![]() m2+m﹣4)=
m2+m﹣4)= ![]() m2﹣
m2﹣ ![]() m+8=
m+8= ![]() (m﹣2)2+
(m﹣2)2+ ![]() ,
,
当m=2时,PM取得最小值 ![]() ,
,
此时,P(2,﹣ ![]() ),
),
对于△PQM,
∵PM⊥x轴,
∴∠QMP=∠DAO=∠AEO,
又∠PQM=90°,
∴△PQM的三个内角固定不变,
∴在动点P运动的过程中,△PQM的三边的比例关系不变,
∴当PM取得最小值时,PQ也取得最小值,
PQ最小=PM最小sin∠QMP=PM最小sin∠AEO= ![]() ×
× ![]() =
= ![]() ,
,
∴当抛物线上的动点P的坐标为(2,﹣ ![]() )时,点P到直线l的距离最小,其最小距离为
)时,点P到直线l的距离最小,其最小距离为 ![]() .
.
【解析】(1)连接AE,由已知得:AE=CE=5,OE=3,利用勾股定理求出OA的长,结合垂径定理求出OC的长,从而得到C点坐标,进而得到抛物线的解析式;(2)求出点D的坐标为(﹣ ![]() ,0),根据△AOE∽△DOA,求出∠DAE=90°,判断出直线l与⊙E相切与A.(3)过点P作直线l的垂线段PQ,垂足为Q,过点P作直线PM垂直于x轴,交直线l于点M.设M(m,
,0),根据△AOE∽△DOA,求出∠DAE=90°,判断出直线l与⊙E相切与A.(3)过点P作直线l的垂线段PQ,垂足为Q,过点P作直线PM垂直于x轴,交直线l于点M.设M(m, ![]() m+4),P(m,﹣
m+4),P(m,﹣ ![]() m2+m﹣4),得到PM=
m2+m﹣4),得到PM= ![]() m+4﹣(﹣
m+4﹣(﹣ ![]() m2+m﹣4)=
m2+m﹣4)= ![]() m2﹣
m2﹣ ![]() m+8=
m+8= ![]() (m﹣2)2+
(m﹣2)2+ ![]() ,根据△PQM的三个内角固定不变,得到PQ最小=PM最小sin∠QMP=PM最小sin∠AEO=
,根据△PQM的三个内角固定不变,得到PQ最小=PM最小sin∠QMP=PM最小sin∠AEO= ![]() ×
× ![]() =
= ![]() ,从而得到最小距离.
,从而得到最小距离.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4). (Ⅰ)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(Ⅱ)以点O为位似中心,将△ABC缩小为原来的 ![]() ,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.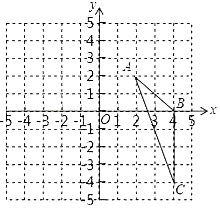
查看答案和解析>>
科目:初中数学 来源: 题型:
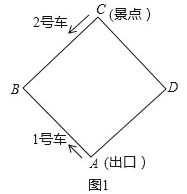
【题目】如图,某景区内的环形路是边长为1200米的正方形ABCD,现有1号、2号两辆游览车分别从出口A和景点C同时出发,1号车沿A→B→C→D→A路线、2号车沿C→B→A→D→C路线连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为300米/分.
(1)如图1,设行驶时间为t分(0≤t≤8)
①1号车、2号车离出口A的路程分别为_____米,_____米;(用含t的代数式表示)
②当两车相距的路程是600米时,求t的值;
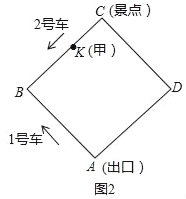
(2)如图2,游客甲在BC上的一点K(不与点B、C重合)处候车,准备乘车到出口A,设CK=x米.
情况一:若他刚好错过2号车,则他等候并搭乘即将到来的1号车;
情况二:若他刚好错过1号车,则他等候并搭乘即将到来的2号车.
请判断游客甲在哪种情况下乘车到出口A用时较多?(含候车时间)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AE平分∠CAB交CD于点E.若∠C比∠AED小55°,则∠AED的度数为( )
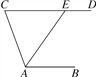
A. 55° B. 125° C. 135° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是( )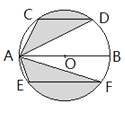
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将-1、![]() 、
、![]() 、2、
、2、![]() 、
、![]() ……按下面的规律排列,若规定(m,n)表示第m排从左至右的第n个数,那么表示(7,2)和(8,4)的数的积是____________.
……按下面的规律排列,若规定(m,n)表示第m排从左至右的第n个数,那么表示(7,2)和(8,4)的数的积是____________.
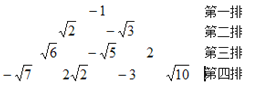
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com